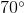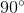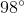The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.)  Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 88 inches for our problem. Its total area would be 88 * 88 or 7744 in².

 Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr² or π * 44² = 1936π in². Therefore, the area remaining would be 7744 – 1936π. The cost of the waste would be 0.25 * (7744 – 1936π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 4 from our subtraction. This would give us: 0.25 * 4 * (1936 – 484π). Since 0.25 is equal to 1/4, 0.25 * 4 = 1. Therefore, our final answer is: 1936 – 484π dollars.

The smallest block from which a circle could be made would be a square that perfectly matches the diameter of the given circle. (This is presuming we have perfectly calibrated equipment.) Such a square would have dimensions equal to the diameter of the circle, meaning it would have sides of 50 inches for our problem. Its total area would be 50 * 50 or 2500 in².

Now, the waste amount would be the "corners" remaining after the circle was cut. The area of the circle is πr² or π * 25² = 625π in². Therefore, the area remaining would be 2500 - 625π. The cost of the waste would be 0.2 * (2500 – 625π). This is not an option for our answers, so let us simplify a bit. We can factor out a common 5 from our subtraction. This would give us: 0.2 * 5 * (500 – 125π). Since 0.2 is equal to 1/5, 0.2 * 625 = 125. Therefore, our final answer is: 500 – 125π dollars.

In order to solve this problem, we need to recall the formula for the circumference of a circle: 

 or 

The circle in this question provides us with the radius, so we can use the first formula to solve:

Solve:

An isosceles triangle not only has two sides of equal measure, it has two angles of equal measure. This means one of two things, which we examine separately:

Case 1: It has another  angle. This is impossible, since a triangle cannot have two obtuse angles.

Case 2: Its other two angles are the ones that are of equal measure. If we let  be their common measure, then, since the sum of the measures of a triangle is , 

Both angles measure 

Since the angles are supplementary, their sum is 180 degrees.  Because they are in a ratio of 1:4, the following expression could be written:

To find the other angle, subtract the given angle from  since complementary angles add up to .

The complementary is:

Supplementary angles add up to . In order to find the correct angle, take the known angle and subtract that from .

The complement to an angle is ninety degrees subtract the angle since two angles must add up to 90.  In this case, since we are given the angle in radians, we are subtracting from  instead to find the complement.  The conversion between radians and degrees is:  

Reconvert the fractions to the least common denominator.

Reduce the fraction.

The two angles at bottom are marked as congruent. One forms a linear pair with a  angle, so it is supplementary to that angle, making its measure .  Therefore, each marked angle measures .

The sum of the measures of the interior angles of a triangle is , so:

The base angles of an isosceles triangle are always equal. Therefore both base angles are .

Let the measure of the third angle. Since the sum of the angles of a triangle is , we can solve accordingly: