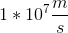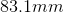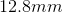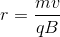For this question, we are being asked to determine the magnetic field necessary to make a particle of a given mass and charge to move in a circular path with a given speed and radius.

To begin with, we can realize that the particle will be moving in a circular path. Thus, there is going to be a centripetal force associated with this circular motion. Moreover, because we know the particle will be present in a magnetic field, we can infer that the magnetic force will be the source of the centripetal force. Thus, we can start by writing out the expression for each of these forces, and then setting them equal to one another.

Rearranging the above expression to isolate the term for magnetic field, we arrive at the following expression.

Now, we can plug in the values given to us in the question stem to solve for the magnetic field strength.

Using

Plugging in values

The equation for finding the force on a moving charged particle in a magnetic field is as follows:

Here,  is the force in Newtons,  is the charge in Coulombs,  is the velocity in , and  is the magnetic field strength in Teslas.

Another way to write the equation without the cross-product is as follows:

Here,  is the angle between the particles velocity and the magnetic field.

For our problem, because theta is ,  evaluates to 1, so we just need to perform multiplication.

Therefore, the force on the particle is 0.3N.

The equation for the force on a current carrying wire in a magnetic field is as follows:

 is the force in Newtons,  is the current in amperes,  is the magnetic field strength in Teslas, and  is the angle from parallel to the magnetic field.

Because our wire is not fully perpendicular to the magnetic field, it does not experience the full possible force. Instead, it experiences  times the maximum force value.

A charged particle moving through a perpendicular magnetic field feels a Lorentz force equal to the formula:

 is the charge,  is the particle speed, and  is the magnetic field strength. This force is always directed perpendicular to the particle’s direction of travel at that moment, and thus acts as a centripetal force. This force is also given by the equation:

We can set these two equations equal to one another, allowing us to solve for the radius of the arc.

Once the particle travels through a semicircle, it is laterally one diameter in distance from where is started (i.e. twice the radius of the circle).

Twice this value is the lateral offset of its crash point from the entrance:

To find the force experienced by the charge, we use this equation:

Because the charge is moving at an angle from perpendicular, we need to take the cross product into account. 

Theta is the angle from perpendicular, which is . Plug in known values and solve.

The equation for force on a charge moving through a magnetic field is:

Because the velocity is perpendicular to the field, the cross product doesn't matter, and we can do simple multiplication.

Therefore, the force on the charge is

The equation for force on a charge moving through a magnetic field is:

.

The cross product is:

Above,  is the degree from parallel the charge is moving. The charge is moving at  from parallel, so the equation, once we plug in our numbers, is:

The force on the charge is about .

The force experienced by a charged particle in a magnetic field is 

This means that when a charge particle is moving perpendicular to the field, due to the cross-product, it experiences the most amount of force (because  is equal to , and theta equals  when it's perpendicular). This means that the charged particle will experience no force due to the magnetic field when it's parallel. We know there will be no force on the particle, and we also know that uncharged particles experience no force in magnetic fields, but we can't say for certain the particle has no net charge, only being told that it's moving parallel to the field.

The rod acts as a battery due to its motion in the magnetic field: . Because there is a closed circuit, this results in current flow:

In this simple circuit, the current is the same everywhere, so the same current flows through the rod. Because of this current, the rod feels a force:

By the right-hand rule, this magnetic force is directed to the left, so the external force must be directed to the right. It is interesting to note that the power dissipated in the resistor:

 is the same as the power provided by the outside force:

The universe conspires to conserve energy.