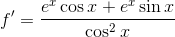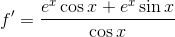We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #35 : Derivative Rules For Sums, Products, And Quotients Of Functions

Differentiate

$y = xe^{2x^2 +1}$

Possible Answers:

$4x^3e^{2x^2+1}$

$e^{2x^2+1}(1+4x^2)$

$4x^3(1+e^{2x^2+1})$

$e^{2x^2+1}+x-1$

$e^{2x^2+1}+4x$

Correct answer:

$e^{2x^2+1}(1+4x^2)$

Explanation:

$y = xe^{2x^2 +1}$

The function is a product of the functions and $e^{2x^2+1}$ , so apply the product rule:

$\frac{dy}{dx}=e^{2x^2+1}\left(\frac{d}{dx}x \right ) +x\left(\frac{d}{dx}e^{2x^2+1} \right )$

The derivative in the first term is The derivative of the second term requires the use of the chain rule.

$\frac{dy}{dx}=e^{2x^2+1} +x\left(4xe^{2x^2+1} \right )$

The derivative in the second term required the use of the chain rule. First we write the derivative of $e^{2x^2+1}$ with respect to the function 2x^2+1 , which is just $e^{2x^2+1}$ . Then we multiply by the derivative of 2x^2+1 with respect to , which is just .

$\frac{d}{dx}e^{2x^2+1}=4xe^{2x^2+1}$

$\frac{dy}{dx}=e^{2x^2+1} +4x^2e^{2x^2+1} = e^{2x^2+1}(1+4x^2)$

Therefore,

$\frac{dy}{dx}= e^{2x^2+1}(1+4x^2)$

Report an Error

Example Question #36 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the following equation:

$h(x)=\frac{6+x^{3}}{x}$

Possible Answers:

$3x^{2}$

$2x+6x^{-2}$

$2x-6x^{2}$

$2x-6x^{-2}$

Correct answer:

$2x-6x^{-2}$

Explanation:

Given that there are 2 terms in the numerator and only one in the denominator, one can split up the equation into 2 separate derivatives:

$\frac{d}{dx}(\frac{6}{x})+\frac{d}{dx}(\frac{x^{3}}{x})$ .

Now we simplify these, and proceed to solve:

$\frac{d}{dx}(6x^{-1})+\frac{d}{dx}(x^{2}) = 2x-6x^{-2}$

Report an Error

Example Question #37 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the following equation:

$h(x)=x\ln(x)$

Possible Answers:

$\ln(x)+1$

$\ln(x)-1$

$\frac{1}{x}$

None of the other answers.

$\frac{-1}{x}$

Correct answer:

$\ln(x)+1$

Explanation:

Because this problem contains two functions multiplied together that can't be simplified any further, it calls for the product rule, which states that

By applying this rule to the equation

$x\ln(x)$

we get

$\frac{d}{dx}(x\ln (x))= ((1)\ln (x)+(x)(\frac{1}{x}))=\ln(x)+1$

Report an Error

Example Question #38 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the following function:

$h(x)=\frac{x}{x^{2}+1}$

Possible Answers:

$\frac{1+x^{2}}{(x^{2}+1)^{2}}$

$\frac{1}{2x}$

$\ln(x+1)$

$\frac{1-x^{2}}{x^{4}+2x^{2}+1}$

None of the other answers

Correct answer:

$\frac{1-x^{2}}{x^{4}+2x^{2}+1}$

Explanation:

Because we are dealing with a quotient that cannot be simplified, we use the quotient rule, which states that if

$h(x)=\frac{f(x)}{g(x)}$ ,

$h{}'(x)=\frac{(g(x)f{}'(x)-f(x)g{}'(x))}{(g(x))^{2}}$ .

By observing the given equation

$h(x)=\frac{x}{x^{2}+1}$ ,

we can see that

f(x)=x

and

$g(x)=x^{2}+1$ .

Therefore, the derivative is

$\frac{(x^{2}+1)(1)-(x)(2x)}{(x^{2}+1)^{2}}=\frac{1-x^{2}}{x^{4}+2x^{2}+1}$ .

Report an Error

Example Question #39 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the following equation:

$h(x)=\frac{x}{\ln (x)}$

Possible Answers:

$\frac{\ln ^{2}(x)}{\ln (x)-1}$

None of the other answers.

$\frac{\ln (x)}{(\ln (x)-1)^{2}}$

$\frac{\ln (x)-1}{\ln ^{2}(x))}$

$\ln(x)-1$

Correct answer:

$\frac{\ln (x)-1}{\ln ^{2}(x))}$

Explanation:

Because we are differentiating a quotient that cannot be simplified, we must use the quotient rule, which states that if

$h(x)=\frac{f(x)}{g(x)}$ ,

then

$h{}'(x)=\frac{g(x)f{}'(x)-f(x)g{}'(x)}{(g(x))^{2}}$ .

By observing the given equation,

$h(x)=\frac{x}{\ln (x)}$ ,

we see that in this case,

f(x)=x

and

$g(x)=\ln(x)$ .

Given this information, the quotient rule tells us that

$h{}'(x)=\frac{\ln (x)(1)-(x)(\frac{1}{x})}{(\ln (x)^{2})}=\frac{\ln (x)-1}{\ln ^{2}(x)}$ .

Report an Error

Example Question #40 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the following equation:

$h(x)=\sin( \frac{x^{2}}{x+1})$

Possible Answers:

$2x\cos(\frac{x^{2}}{x+1})$

$\frac{x(x+2)}{(x+3)^{2}}\cos(\frac{x^{2}}{x+1})$

None of the other answers.

$\frac{x(x+2)}{(x+1)^{2}}\cos(\frac{x^{2}}{x+1})$

$\cos(\frac{x^{2}}{x+1})$

Correct answer:

$\frac{x(x+2)}{(x+1)^{2}}\cos(\frac{x^{2}}{x+1})$

Explanation:

This problem is a quotient rule inside of a chain rule. First, let's look at the chain rule:

Given this, we can deduce that since

$h(x)=\sin(\frac{x^{2}}{x+1})$ ,

$f(x)=\sin(x)$

and

$g(x)=\frac{x^{2}}{x+1}$ .

By plugging these into the chain rule formula, we get

$(f o g(x)){}'=\cos(\frac{x^{2}}{x+1})((\frac{d}{dx}(\frac{x^{2}}{x+1})))$

To find the derivative of the

second term, we must use the quotient rule, which states that the the derivative

of a quotient is ((denominator)(derivative of numerator)-(numerator)(derivative

of denominator))/(denominator squared). Using this rules we find that

$\frac{d}{dx}(\frac{x^{2}}{x+1})=\frac{((x+1)(2x)-(x^{2})(1))}{(x+1)^{2}}=\frac{x(x+2)}{(x+1)^{2}}$ .

By plugging this back in, we find the final derivative to be

$\frac{x(x+2)}{(x+1)^{2}}\cos(\frac{x^{2}}{x+1})$

Report an Error

Example Question #244 : Computation Of The Derivative

Find the derivative of the function:

$f=\frac{\tan(x)+5}{x}$

Possible Answers:

$\frac{x\sec^2(x)-\tan(x)-5}{x}$

$\frac{x\sec(x)-\tan(x)-5}{x^2}$

$\frac{x\sec^2(x)-\tan(x)-5}{x^2}$

$\frac{x\sec^2(x)-\tan(x)+5}{x^2}$

Correct answer:

$\frac{x\sec^2(x)-\tan(x)-5}{x^2}$

Explanation:

The derivative of the function is equal to

$f'=\frac{x\sec^2(x)-\tan(x)-5}{x^2}$

and was found using the following rules:

$\frac{\mathrm{d} }{\mathrm{d} x} \frac{f(x)}{g(x)}=\frac{g(x)f'(x)-f(x)g'(x)}{g(x)^2}$ , $\frac{\mathrm{d} }{\mathrm{d} x} \tan(x)=\sec^2(x)$ , $\frac{\mathrm{d} }{\mathrm{d} x} ax=a$

Report an Error

Example Question #41 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function

$f=\frac{e^x}{\cos{x}}$

Possible Answers:

$f'=\frac{e^x\cos{x}-e^x\sin{x}}{\cos^2{x}}$

$f'=\frac{e^x\cos{x}+e^x\sin{x}}{\cos{x}}$

$f'=\frac{e^x\cos{x}+e^x\cos{x}}{\cos^2{x}}$

$f'=\frac{e^x\cos{x}+e^x\sin{x}}{\cos^2{x}}$

Correct answer:

$f'=\frac{e^x\cos{x}+e^x\sin{x}}{\cos^2{x}}$

Explanation:

To find the derivative of a quotient, you apply the quotient rule:

$\frac{\mathrm{d} }{\mathrm{d} x}(\frac{f(x)}{g(x)})=\frac{{f'(x)g(x)-f(x)g'(x)}}{(g(x))^2}$

In our case, we have f(x)=e^x and $g(x)=\cos{x}$

Using the function from the problem statement and taking its derivative, we get

$f'=\frac{e^x\cos{x}+e^x\sin{x}}{\cos^2{x}}$

Report an Error

Example Question #42 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function

$f=\frac{\cos{x}}{2x^2}$

Possible Answers:

$f'=\frac{-2x^2\sin{x}-4x\cos{x}}{2x^4}$

$f'=\frac{-2x^2\sin{x}-4x\sin{x}}{4x^4}$

$f'=\frac{-x^2\sin{x}-4x\cos{x}}{2x^4}$

$f'=\frac{-2x^2\sin{x}-4x\cos{x}}{4x^4}$

Correct answer:

$f'=\frac{-2x^2\sin{x}-4x\cos{x}}{4x^4}$

Explanation:

To find the derivative of a quotient, you apply the quotient rule:

$\frac{\mathrm{d} }{\mathrm{d} x}(\frac{f(x)}{g(x)})=\frac{{f'(x)g(x)-f(x)g'(x)}}{(g(x))^2}$

In our case, we have $f(x)=\cos{x}$ and g(x)=2x^2

Using the function from the problem statement and taking its derivative, we get

$f'=\frac{-2x^2\sin{x}-4x\cos{x}}{4x^4}$

Report an Error

Example Question #43 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative of the function

$f=2x\sin{x}+2\cos{x}$

Possible Answers:

$f'=2x\cos{x}$

$f'=2x\cos{x}+2\sin{x}$

$f'=-2x\cos{x}$

$f'=2\cos{x}$

Correct answer:

$f'=2x\cos{x}$

Explanation:

To find the derivative of the function, you must apply the product rule. The product rule is as follows

$\frac{\mathrm{d} }{\mathrm{d} x}(f(x)g(x))=f'(x)g(x)+f(x)g'(x)$

In the first part of the expression, we have f(x)=2x and $g(x)=\sin{x}$ , and in the second part of the expression we have f(x)=2 and $g(x)=\cos{x}$

Using the product rule from above, we have

$f'=2\sin{x}+2x\cos{x}-2\sin{x}=2x\cos{x}$

Report an Error

View AP Calculus AB Tutors

Ping
Certified Tutor

The University of Texas at Dallas, Bachelor of Science, Computer Science. University of North Texas, Master of Arts, Education.

View AP Calculus AB Tutors

Amanda
Certified Tutor

Seattle University, Current Undergrad Student, Applied Mathematics.

View AP Calculus AB Tutors

Magdy
Certified Tutor

Cairo University, Egypt, Bachelor of Science, Electrical Engineering. New Mexico State University-Main Campus, Doctor of Phil...

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in Seattle, SSAT Tutors in San Francisco-Bay Area, Chemistry Tutors in Philadelphia, LSAT Tutors in Washington DC, Computer Science Tutors in Phoenix, ACT Tutors in Houston, SSAT Tutors in Miami, English Tutors in San Diego, GMAT Tutors in Dallas Fort Worth, MCAT Tutors in Phoenix

Popular Courses & Classes

MCAT Courses & Classes in Dallas Fort Worth, GRE Courses & Classes in Boston, Spanish Courses & Classes in Phoenix, ACT Courses & Classes in Los Angeles, MCAT Courses & Classes in Houston, LSAT Courses & Classes in San Francisco-Bay Area, Spanish Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Seattle, ACT Courses & Classes in Atlanta, Spanish Courses & Classes in Philadelphia

Popular Test Prep

ISEE Test Prep in Denver, SAT Test Prep in Denver, GMAT Test Prep in Boston, SAT Test Prep in Chicago, ACT Test Prep in Los Angeles, SAT Test Prep in Boston, MCAT Test Prep in Miami, MCAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Philadelphia, SSAT Test Prep in Atlanta

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #35 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #36 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #37 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #38 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #39 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #40 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #244 : Computation Of The Derivative

Example Question #41 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #42 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #43 : Derivative Rules For Sums, Products, And Quotients Of Functions

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: