All AP Calculus AB Resources
Example Questions
Example Question #1 : Mean Value Theorem
As a consequence of the Mean Value Theorem, there must be a value 
By the Mean Value Theorem (MVT), if a function 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/976401/gif.latex)





Evaluating 

The expression for 

the correct choice.
Example Question #55 : Derivative As A Function


The values of 

Which of the following is a consequence of Rolle's Theorem?




There cannot be 

There must be 

None of the statements in the other choices follows from Rolle's Theorem.
There must be 

By Rolle's Theorem, if 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969995/gif.latex)









Incidentally, it does follow from the given information that 

Example Question #8 : Mean Value Theorem
Find the mean value of the function 

To find the mean value of a function over some interval 

Plugging in
Simplifying
One must then use the inverse Sine function to find the value c:

Example Question #2 : Continunity As A Property Of Functions
If 
We cannot conclude any of the other answers.






We cannot conclude any of the other answers.
Unless we are explicitly told so, via graph, information, or otherwise, we cannot assume 




We cannot assume anything about the existence of 

Example Question #1 : Understanding Continuity In Terms Of Limits
Which of the following is equal to 


The limit of a function as 




Example Question #2 : Understanding Continuity In Terms Of Limits
Determine any points of discontinuity for the function:
For a function to be continuous the following criteria must be met:
- The function must exist at the point (no division by zero, asymptotic behavior, negative logs, or negative radicals).
- The limit must exist.
- The point must equal the limit. (Symbolically,
).
It is easiest to first find any points where the function is undefined. Since our function involves a fraction and a natural log, we must find all points in the domain such that the natural log is less than or equal to zero, or points where the denominator is equal to zero.
To find the values that cause the natural log to be negative we set
Therefore, those x values will yield our points of discontinuity. Normally, we would find values where the natural log is negative; however, for all 
Example Question #1 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find the derivative of the function,
Differentiate both sides and proceed with the product rule:
![\frac{dy}{dx}=\frac{d}{dx}[x^2\sin(3x)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/749291/gif.latex)
Evaluate the derivatives in each term. For the first term,

apply the chain rule,
So now the first term in equation (2) can be written,
![x^2\frac{d}{dx}\sin(3x)=x^2[3\cos(3x)]=3x^2\cos(3x)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741374/gif.latex)
The second term in equation (2) is easy, this is just the product of 


Combine equations (3) and (4) to write the derivative,
Example Question #201 : Computation Of The Derivative
Find the derivative.
Use the product rule to find the derivative.
Example Question #3 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find the derivative.
Use the power rule to find the derivative.
Thus, the derivative is
Example Question #4 : Derivative Rules For Sums, Products, And Quotients Of Functions
Find 
Here we use the product rule:
Let 
Then 
and 
Subbing these values back into our equation gives us
Simplify by combining like-terms
and pulling out a 
All AP Calculus AB Resources
























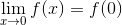




















![\frac{dy}{dx} =x[3x\cos(3x)+2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/741367/gif.latex)