We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

Create An Account

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #228 : Computation Of The Derivative

Find f'(x) for the following f(x).

$f(x)=4^{x}cot(x)$

Possible Answers:

$f'(x)=ln(4)\cdot cot(x)-4^{x}csc^{2}x$

$f'(x)=ln(4)\cdot 4^{x}\cdot cot(x)-4^{x}sec^{2}x$

$f'(x)=4^{x}ln(4)cot(x)-4^{x}csc^{2}x$

$f'(x)= 4^{x}\cdot cot(x)-4^{x}csc^{2}x$

$f'(x)=ln(4)\cdot 4^{x}\cdot cot(x)+4^{x}csc^{2}x$

Correct answer:

$f'(x)=4^{x}ln(4)cot(x)-4^{x}csc^{2}x$

Explanation:

Since the function f(x) is a product of two functions, 4^x and cot(x), use the product rule to take this derivative.

Recall the product rule where u and v are two separate functions:

(uv)'=u'v+uv'

Let's define u and v as follows:

$u=4^{x}$

v=cot(x)

Take the derivative of u and v:

$u'=4^{x}ln(4)$

$v'=-csc^{2}x$

Now that we've found values of u, u', v, and v' we can substitute them into the product formula for the final answer.

$f'(x)=(uv)'=u'v+uv'=4^{x}ln(4) cot(x)-4^{x}csc^{2}x$

Report an Error

Example Question #229 : Computation Of The Derivative

Find f'(x) for the following f(x).

$f(x)=\frac{tanx}{e^{x}}$

Possible Answers:

$f'(x)=\frac{sec^{2}x-2\cdot tanx}{e^{x}}$

$f'(x)=\frac{sec^{2}x+e^{x}\cdot tanx}{e^{2x}}$

$f'(x)=\frac{sec^{2}x-tanx}{e^{x}}$

$f'(x)=\frac{e^{x}sec^{2}x-tanx}{e^{2x}}$

$f'(x)=\frac{sec^{2}x+tanx}{e^{2x}}$

Correct answer:

$f'(x)=\frac{sec^{2}x-tanx}{e^{x}}$

Explanation:

Since the function f(x) is a quotient of two separate functions, tan(x) and e^x, use the quotient rule to take the derivative.

Recall the quotient rule for two functions u and v:

$(\frac{u}{v})^{'}=\frac{u'v-uv'}{v^{2}}$

Let's define u and v for this function as follows:

u=tan(x)

$v=e^{x}$

Take the derivative of u and v:

$u'=sec^{2}x$

$v'=e^{x}$

Now that we've defined u, u', v, and v' we can substitute them into the quotient rule formula.

$(\frac{u}{v})^{'}=\frac{u'v-uv'}{v^{2}}=\frac{sec^{2}(x) e^{x}-tan(x)e^{x}}{e^{2x}}$

Divide the numerator and denominator by e^x for the answer in its final form.

$f'(x)=\frac{sec^{2}x-tanx}{e^{x}}$

Report an Error

Example Question #230 : Computation Of The Derivative

Find f'(x) for the following f(x).

$f(x)=\frac{x^{4}}{x^{3}+1}$

Possible Answers:

$f'(x)=\frac{7x^{6}+4x^{3}}{(x^{3}+1)^{3}}$

$f'(x)=\frac{x^{6}-4x^{3}}{(x^{3}+1)^{2}}$

$f'(x)=\frac{x^{6}+4x^{3}}{(x^{3}+1)^{2}}$

$f'(x)=\frac{x^{6}+4x^{3}}{(x^{3}-1)^{2}}$

$f'(x)=\frac{x^{6}+4x^{3}+1}{(x^{3}+1)^{2}}$

Correct answer:

$f'(x)=\frac{x^{6}+4x^{3}}{(x^{3}+1)^{2}}$

Explanation:

Since the function f(x) is a quotient of two separate functions, x^4 and x^3+1, use the quotient rule to take the derivative.

Recall the quotient rule for two functions u and v:

$(\frac{u}{v})^{'}=\frac{u'v-uv'}{v^{2}}$

Let's define u and v for this function as follows:

u=x^4

$v=x^{3}+1$

Take the derivative of u and v:

$u'=4x^{3}$

$v'=3x^{2}$

Now that we've defined u, u', v, and v' we can substitute them into the quotient rule formula.

$(\frac{u}{v})^{'}=\frac{4x^{3}(x^{3}+1)-x^{4}3x^{2}}{(x^{3}+1)^{2}}$

Distribute the 4x^3 and simplify for the final answer.

$f'(x)=\frac{x^{6}+4x^{3}}{(x^{3}+1)^{2}}$

Report an Error

Example Question #21 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find f'(x) for the following f(x).

$f(x)=\frac{10^{x}}{cos(x)}$

Possible Answers:

$f'(x)=\frac{10^{x}(ln(10)cos(x)+sin(x))}{cos^{2}x}$

$f'(x)=\frac{10^{x}(ln(10)cos(x)-sin(x))}{cos^{2}x}$

$f'(x)=\frac{10^{x}(10\cdot cos(x)+sin(x))}{cos^{2}x}$

$f'(x)=\frac{10^{x}(ln(10)cos(x)+sin(x))}{sin^{2}x}$

$f'(x)=\frac{10^{x}(ln(x)cos(x)+sin(x))}{cos^{2}x}$

Correct answer:

$f'(x)=\frac{10^{x}(ln(10)cos(x)+sin(x))}{cos^{2}x}$

Explanation:

Since the function f(x) is a quotient of two separate functions, 10^x and cos(x), use the quotient rule to take the derivative.

Recall the quotient rule for two functions u and v:

$(\frac{u}{v})^{'}=\frac{u'v-uv'}{v^{2}}$

Let's define u and v for this function as follows:

$u=10^{x}$

v=cos(x)

Take the derivative of u and v:

$u'=ln(10)10^{x}$

v'=-sin(x)

Now that we've defined u, u', v, and v' we can substitute them into the quotient rule formula for the final answer.

$(\frac{u}{v})^{'}=\frac{u'v-uv'}{v^{2}}=f'(x)=\frac{10^{x}(ln(10)cos(x)+sin(x))}{cos^{2}x}$

Report an Error

Example Question #22 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find f'(x) for the following f(x).

$f(x)=3x^{7}-x^{10}\cdot sin(x)$

Possible Answers:

$f'(x)=21x^{6}-10x^{9}sin(x)-x^{10}sin(x)$

$f'(x)=21x^{6}+10x^{9}cos(x)-x^{10}sin(x)$ e

$f'(x)=21x^{6}-10x^{9}sin(x)+x^{10}cos(x)$

$f'(x)=21x^{6}-10x^{9}sin(x)-x^{10}cos(x)\cdot 10x^{9}$

$f'(x)=21x^{6}-10x^{9}sin(x)-x^{10}cos(x)$

Correct answer:

$f'(x)=21x^{6}-10x^{9}sin(x)-x^{10}cos(x)$

Explanation:

The function f(x) is a sum of two functions, 3x^7 and -x^10*sin(x). When functions are added together, take the derivative of each one separately. First take the derivative of 3x^7:

$\frac{d}{dx}3x^{7}=21x^{6}$

The second part of the function, -x^10*sin(x) is a product of two functions so use the product rule to take the derivative. Recall the product rule where u and v are two separate functions:

(uv)'=u'v+uv'

Let's define u and v as follows:

$u=-x^{10}$

v=sin(x)

Take the derivative of u and v:

$u'=-10x^{9}$

v'=cos(x)

Now that we've found values of u, u', v, and v' substitute them into the product rule formula.

$(uv)'=u'v+uv'=-10x^{9}sin(x)-x^{10}cos(x)$

For the final answer add (uv)' to the derivative of 3x^7.

$f'(x)=21x^{6}-10x^{9}sin(x)-x^{10}cos(x)$

Report an Error

Example Question #23 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find f'(x) for the following f(x).

$f(x)=\frac{cosx}{x^2+1}$

Possible Answers:

$f'(x)=\frac{-sinx(x)x^{2}-2xcosx}{(x^{2}+1)^{2}}$

$f'(x)=\frac{-cosx(x^{2}+1)-2xsinx}{(x^{2}+1)^{2}}$

$f'(x)=\frac{-sinx(x)(x^{2}+1)-2xcosx}{(x^{2}+1)^{2}}$

$f'(x)=\frac{-sinx(x)(x^{2}+1)+2x}{(x^{2}+1)^{2}}$

$f'(x)=\frac{sinx(x)(x^{2}+1)+2xcosx}{(x^{2}+1)^{2}}$

Correct answer:

$f'(x)=\frac{-sinx(x)(x^{2}+1)-2xcosx}{(x^{2}+1)^{2}}$

Explanation:

Since the function f(x) is a quotient of two separate functions, cos(x) and x^2+1, use the quotient rule to take the derivative.

Recall the quotient rule for two functions u and v:

$(\frac{u}{v})^{'}=\frac{u'v-uv'}{v^{2}}$

Let's define u and v for this function as follows:

u=cosx

$v=x^{2}+1$

Take the derivative of u and v:

u'=-sinx

v'=2x

Now that we've defined u, u', v, and v' we can substitute them into the quotient rule formula for the final answer.

$f'(x)=(\frac{u}{v})^{'}=\frac{-sinx(x^{2}+1)-cosx \cdot 2x}{(x^{2}+1)^{2}}$

Report an Error

Example Question #31 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find f'(x) for the following f(x).

$f(x)=\frac{sinx+cosx}{e^{x}}$

Possible Answers:

$f'(x)=\frac{-2cosx}{e^{x}}$

$f'(x)=\frac{-2sinx}{e^{2x}}$

$f'(x)=\frac{-2e^{x}sinx}{e^{x}}$

$f'(x)=\frac{-2sinx}{e^{x}}$

$f'(x)=\frac{sinx}{e^{2x}}$

Correct answer:

$f'(x)=\frac{-2sinx}{e^{x}}$

Explanation:

Since the function f(x) is a quotient of two separate functions, sin(x) + cos(x) and e^x, use the quotient rule to take the derivative.

Recall the quotient rule for two functions u and v:

$(\frac{u}{v})^{'}=\frac{u'v-uv'}{v^{2}}$

Let's define u and v for this function as follows:

u=sinx+cosx

$v=e^{x}$

Take the derivative of u and v:

u'=cosx-sinx

$v'=e^{x}$

Now that we've defined u, u', v, and v' we can substitute them into the quotient rule formula.

$f'(x)=(\frac{u}{v})^{'}=\frac{(cosx-sinx)e^{x}-(sinx+cosx)e^{x}}{e^{2x}}$

Factor out e^x from to the top and bottom and simplify into the final form:

$f'(x)=\frac{-2sinx}{e^{x}}$

Report an Error

Example Question #32 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find f'(x) for the following f(x).

$f(x)=5x^{4}\cdot sec(x)$

Possible Answers:

$f'(x)=20x^{3}\cdot sec(x)\cdot tan(x)$

$f'(x)=20x^{3}\cdot sec(x)+5x^{4}\cdot sec(x)\cdot tan(x)$

$f'(x)= sec(x)+5x^{4}$

$f'(x)=20x^{3}+ sec(x)\cdot tan(x)$

$f'(x)=20x^{3}-5x^{4}\cdot sec(x)\cdot tan(x)$

Correct answer:

$f'(x)=20x^{3}\cdot sec(x)+5x^{4}\cdot sec(x)\cdot tan(x)$

Explanation:

Since the function f(x) is a product of two functions, 5x^4 and sec(x), use the product rule to take this derivative.

Recall the product rule where u and v are two separate functions:

(uv)'=u'v+uv'

Let's define u and v as follows:

$u=5x^{4}$

v=sec(x)

Take the derivative of u and v:

$u'=20x^{3}$

$v'=sec(x)\cdot tan(x)$

Now that we've found values of u, u', v, and v' we can substitute them into the product rule formula for the final answer.

$f'(x)=(uv)'=u'v+uv'=20x^{3}\cdot sec(x)+5x^{4}\cdot sec(x)\cdot tan(x)$

Report an Error

Example Question #33 : Derivative Rules For Sums, Products, And Quotients Of Functions

Differentiate the function:

$y=x^2\sqrt{3x+1}$

Possible Answers:

$2x\sqrt{3x+1}+\frac{1}{2}(3x+1)$

$= \frac{x(13x+2)}{\sqrt{3x+1}}+1$

$\frac{x}{2\sqrt{3x+1}}$

$3\sqrt{3x+1}+\frac{1}{2}(3x+1)^{-1/2}$

$= \frac{x(15x+4)}{2\sqrt{3x+1}}$

Correct answer:

$= \frac{x(15x+4)}{2\sqrt{3x+1}}$

Explanation:

$y = x^2 \sqrt{3x+1}$

First notice that the function is a product of two functions x^2 and $\sqrt{3x+1}$ . Apply the product rule:

$\frac{dy}{dx}=\sqrt{3x+1}\left(\frac{d}{dx}x^2 \right )+x^2\left(\frac{d}{dx}\sqrt{3x+1} \right )$

_______________________________________________________________

The second term will require the chain rule. Recall that the derivative for a radical function-of-a-function $y=\sqrt{u(x)}$ is given by:

$\underset{Chain-Rule}{ \underbrace{\frac{dy}{dx}=\frac{dy}{du}\frac{du}{dx}}} =\frac{1}{2\sqrt{u(x)}}u'(x)$

_______________________________________________________________

$\frac{dy}{dx}=\sqrt{3x+1}(2x )+x^2\left(\frac{3}{2\sqrt{3x+1}}\right)$

$=2x\sqrt{3x+1}+\frac{3x^2}{2\sqrt{3x+1}}$

$= \frac{2x\sqrt{3x+1}(2\sqrt{3x+1} )+3x^2}{2\sqrt{3x+1}}$

$= \frac{4x(3x+1)+3x^2}{2\sqrt{3x+1}}$

$= \frac{12x^2+4x+3x^2}{2\sqrt{3x+1}}$

$= \frac{15x^2+4x}{2\sqrt{3x+1}}$

Report an Error

Example Question #34 : Derivative Rules For Sums, Products, And Quotients Of Functions

Find the derivative $\frac{dy}{dx}$

$y= \frac{2x-1}{\sqrt{x^2+4}}$

Possible Answers:

$=\frac{x-1}{x^2+4 }$

$=\frac{x+8}{(x^2+4)^{3/2}}$

$=\frac{x-4}{(x^2+4)^{3/2}}$

$=\frac{2(x-4)}{\sqrt{x^2 +4}}+1$

$=\frac{x+2}{(x^2+4)^{2}}$

Correct answer:

$=\frac{x+8}{(x^2+4)^{3/2}}$

Explanation:

$y= \frac{2x-1}{\sqrt{x^2+4}}$

The derivative can be computed using the quotient rule:

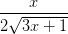
$y = \frac{f(x)}{g(x)}\: \: \: \: \: \:\ \Rightarrow \: \: \: \: \: \:\frac{dy}{dx}=\frac{g(x)f'(x)-g'(x)f(x)}{[g(x)]^2 }$

$\frac{dy}{dx}=\frac{\sqrt{x^2+4}\left[\frac{d}{dx}(2x-1) \right ]-\left[\frac{d}{dx}\sqrt{x^2+4} \right ](2x-1)}{x^2+4}$

$=\frac{2\sqrt{x^2+4}-\frac{1}{2\sqrt{x^2+4}}(2x)(2x-1)}{x^2+4}$

$=\frac{2\sqrt{x^2+4}-\frac{2x^2-x}{\sqrt{x^2+4}}}{x^2+4}$

$=\frac{2(x^2+4)-(2x^2-x)}{\sqrt{x^2+4}(x^2+4)}$

$=\frac{x+8}{(x^2+4)^{3/2}}$

Report an Error

View AP Calculus AB Tutors

Leonid
Certified Tutor

Polytechnic Institute of Bucharest, Romania, Bachelor of Science, Avionics Maintenance Technology. Bucharest Academy of Econo...

View AP Calculus AB Tutors

Ranjeeta
Certified Tutor

University of Rajasthan, Bachelor of Science, Mathematics. University of Rajasthan, Master of Science, Mathematics.

View AP Calculus AB Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

All AP Calculus AB Resources

3 Diagnostic Tests 164 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

LSAT Tutors in Houston, SAT Tutors in Seattle, English Tutors in Washington DC, ACT Tutors in Los Angeles, GMAT Tutors in Denver, Computer Science Tutors in Denver, Reading Tutors in Los Angeles, GRE Tutors in Los Angeles, SSAT Tutors in Denver, SAT Tutors in San Diego

Popular Courses & Classes

SSAT Courses & Classes in Phoenix, SAT Courses & Classes in Dallas Fort Worth, MCAT Courses & Classes in Los Angeles, Spanish Courses & Classes in Miami, GRE Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Washington DC, MCAT Courses & Classes in Philadelphia, MCAT Courses & Classes in Atlanta, ACT Courses & Classes in Miami, LSAT Courses & Classes in Denver

Popular Test Prep

ISEE Test Prep in Seattle, GRE Test Prep in Seattle, LSAT Test Prep in Los Angeles, SSAT Test Prep in Phoenix, ISEE Test Prep in San Francisco-Bay Area, MCAT Test Prep in Chicago, ISEE Test Prep in Washington DC, MCAT Test Prep in Los Angeles, SAT Test Prep in Miami, ACT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

AP Calculus AB : AP Calculus AB

Study concepts, example questions & explanations for AP Calculus AB

All AP Calculus AB Resources

Example Questions

Example Question #228 : Computation Of The Derivative

Example Question #229 : Computation Of The Derivative

Example Question #230 : Computation Of The Derivative

Example Question #21 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #22 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #23 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #31 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #32 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #33 : Derivative Rules For Sums, Products, And Quotients Of Functions

Example Question #34 : Derivative Rules For Sums, Products, And Quotients Of Functions

All AP Calculus AB Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: