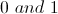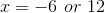We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #971 : Algebra Ii

Which of the below quadratic functions will be the widest?

Possible Answers:

f(x)=10x^2+5x-4

$f(x)=\frac{2}{3}x^2+5x-3$

$f(x)=\frac{1}{8}(x-2)^2$

f(x)=5x^2+7

Correct answer:

$f(x)=\frac{1}{8}(x-2)^2$

Explanation:

To determine how "wide" or "skinny" a parabola is, we look at the leading coefficient.

The smaller the fraction, the wider a parabola will be.

The larger the whole number, the skinnier the parabola will be.

$In\ this\ case\ the\ smallest\ fractional\ leading\ coefficient\ was\ the\ \frac{1}{8}$

This will give us the widest parabola.

Report an Error

Example Question #41 : Quadratic Functions

Shift y=3(3x-1)^2+1 up one unit. What is the new equation?

Possible Answers:

y= 27x^2+18x+8

y=27x^2+1

y= 27x^2-18x+8

y= 27x^2-18x+5

y=27x^2+2

Correct answer:

y= 27x^2-18x+5

Explanation:

Simplify the following equation by using the FOIL method with the binomial.

(3x-1)^2 = (3x)(3x)+(3x)(-1)+(-1)(3x)+(-1)(-1)

Simplify all terms in the parentheses.

9x^2-3x-3x+1 = 9x^2-6x+1

Replace the term and simplify.

y=3(9x^2-6x+1)+1

y=27x^2-18x+3+1 = 27x^2-18x+4

The equation in standard form is: y= 27x^2-18x+4

Since this parabola is shifted up one unit, add one to the y-intercept.

The answer is: y= 27x^2-18x+5

Report an Error

Example Question #45 : Quadratic Functions

Write the equation for the parabola y = x^2 + 5x - 7 after it has been reflected over the y-axis, then shifted up 2 and left 4.

Possible Answers:

y=-x^2 -13x - 31

y = x^2 + 3x -9

y = -x^2 - 13x - 41

y = x^2 + 13x + 41

y = -x^2 +5x + 25

Correct answer:

y = x^2 + 3x -9

Explanation:

First, reflect the equation over the y-axis by switching the sign of x:

y = (-x)^2 + 5(-x) - 7 = x^2 -5x - 7

Now shift up 2 by adding 2:

y = x^2 - 5x - 7 + 2 = x^2 -5x - 5

Now shift left 4 by adding 4 to x:

y = (x+4)^2 - 5(x + 4 ) - 5 first expand (x+4)^2

(x+4 )(x+4) = x^2 + 4x + 4x + 16 = x^2 + 8x + 16

Now multiply -5(x+4) = -5x - 20

Now plug those back in:

y = x^2 + 8x + 16 - 5x - 20 - 5 combine like terms

y = x^2 + 3x -9

Report an Error

Example Question #1 : Circle Functions

Find the -intercepts for the circle given by the equation:

(x-1)^2+y^2=9

Possible Answers:

$0\ and\ 9$

$-4\ and\ 2$

$0\ and\ 1$

$-2\ and\ 4$

$1\ and\ 9$

Correct answer:

$-2\ and\ 4$

Explanation:

To find the -intercepts (where the graph crosses the -axis), we must set y=0 . This gives us the equation:

(x-1)^2=9

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

$x-1=\sqrt{9}$ and $x-1=-\sqrt{9}$

We can then solve these two equations to obtain $x=-2\ or\ 4$ .

Report an Error

Example Question #972 : Algebra Ii

Find the -intercepts for the circle given by the equation:

(x-3)^2+(y+5)^2=106

Possible Answers:

$12\ and\ 6$

$-6\ and\ 12$

$-3\ and\ 5$

$8\ and\ 12$

$3\ and\ -5$

Correct answer:

$-6\ and\ 12$

Explanation:

To find the -intercepts (where the graph crosses the -axis), we must set y=0 . This gives us the equation:

(x-3)^2+25=106

(x-3)^2=81

$x-3=\sqrt{81}=9$ and $x-3=-\sqrt{81}=-9$

We can then solve these two equations to obtain

$x=-6\ or\ 12$

Report an Error

Example Question #973 : Algebra Ii

What is the greatest possible value of the -coordinate?

$(x-3)^{2} + (y+4)^{2} = 36$

Possible Answers:

Correct answer:

Explanation:

This equation describes a circle of radius (square root of ), centered at the point (3,-4) . The equation (which is NOT a function) has a maximum y-coordinate value directly above the center of the circle in the vertical direction. Take the y-coordinate of the center, , and add to it the length of the radius, , to get the answer, .

Report an Error

Example Question #1 : Circle Functions

Find the intercept of a circle.

$( x - 5 )^{2} + ( y + 6)^2 = 40$

Possible Answers:

-7, -3

6, 14

7, 3

-5, 6

-5, 14

Correct answer:

7, 3

Explanation:

$( x - 5)^{^{2}} + ( y + 6 )^{2} = 40$

Let

y = 0

Therefore the equation becomes,

$\left ( x - 5 \right )^{2} + \left ( 0 + 6 \right )^{2} = 40$

Solve for x.

$(x - 5)^{2} + 36 = 40$

-36 -36

$\sqrt{(x - 5)}^{2} = \pm \sqrt{4}$

$x - 5 = \pm 2$

+ 5 + 5

x = 5 + 7

x = 7

x = 5 - 2

x = 3

Report an Error

Example Question #3 : Circle Functions

Find the intercept of a circle.

$(x - 4)^{2} + (y - 6)^{2} = 20$

Possible Answers:

7, 8

8, 4

4, 7

-8, -4

-4, 7

Correct answer:

8, 4

Explanation:

$(x - 4)^{2} + (y - 6)^{2} = 20$

Let

x = 0

Therefore, the equation becomes:

$(0 - 4)^{2} + (y - 6)^{^{2}} = 20$

Solve for y.

$= 16 + (y - 6)^{2} = 20$

-16 -16

$\sqrt{(y - 6)^{2}} = \pm \sqrt{4}$

$y - 6 = \pm 2$

+6 +6

$y = 6 \pm 2$

y = 6 + 2 = 8

y = 6 - 2 = 4

Report an Error

Example Question #52 : Quadratic Functions

A circle centered at (3, 7) has a radius of units.

What is the equation of the circle?

Possible Answers:

(x-3)^2+(y-7)^2=9

(x-3)^2+(y-7)^2=3

(x+3)^2+(y+7)^2=9

(x-3)+(y-7)=9

Correct answer:

(x-3)^2+(y-7)^2=9

Explanation:

The equation for a circle centered at the point (h, k) with radius r units is

(x-h)^2+(y-k)^2=r^2 .

Setting h=3 , k=7 , and r=3 yields

(x-3)^2+(y-7)^2=3^2

(x-3)^2+(y-7)^2=9 .

Report an Error

Example Question #5 : Circle Functions

Convert the following angle to radians

$\measuredangle135$

Possible Answers:

$\frac{\Pi}{4}$

$\frac{4\Pi }{3}$

$\frac{3\Pi }{4}$

$\frac{\Pi }{2}$

$2\frac{\Pi }{3}$

Correct answer:

$\frac{3\Pi }{4}$

Explanation:

To convert degrees to radians, multiply degrees by:

$\frac{\Pi }{180}$

$135*\frac{\Pi }{180}=\frac{135\Pi }{180} \rightarrow Simplified: \frac{135}{180}=\frac{3}{4}$

Therefore $\frac{135\Pi }{180} = \frac{3\Pi }{4}$

Report an Error

View Algebra 2 Tutors

Anne
Certified Tutor

University of Maryland-Baltimore, Doctor of Science, Accounting.

View Algebra 2 Tutors

Delilah
Certified Tutor

Emory University, Bachelor in Arts, Political Science and Government.

View Algebra 2 Tutors

Dianne
Certified Tutor

University of the Virgin Islands, Bachelor in Arts, Mathematics. University of South Carolina-Aiken, Master of Arts, Mathemat...

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

ACT Tutors in San Diego, English Tutors in Atlanta, Reading Tutors in Denver, Biology Tutors in Washington DC, Reading Tutors in New York City, Calculus Tutors in Houston, English Tutors in Washington DC, ACT Tutors in San Francisco-Bay Area, MCAT Tutors in Seattle, SAT Tutors in Houston

Popular Courses & Classes

MCAT Courses & Classes in Philadelphia, ISEE Courses & Classes in Atlanta, ISEE Courses & Classes in Chicago, LSAT Courses & Classes in Atlanta, GMAT Courses & Classes in Seattle, Spanish Courses & Classes in Atlanta, ACT Courses & Classes in Los Angeles, ACT Courses & Classes in Chicago, GRE Courses & Classes in Chicago, GMAT Courses & Classes in Miami

Popular Test Prep

SSAT Test Prep in Dallas Fort Worth, ACT Test Prep in Chicago, ISEE Test Prep in San Francisco-Bay Area, SSAT Test Prep in Houston, ACT Test Prep in San Francisco-Bay Area, ACT Test Prep in Los Angeles, LSAT Test Prep in Phoenix, SAT Test Prep in Denver, GRE Test Prep in Miami, SAT Test Prep in Houston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #971 : Algebra Ii

Which of the below quadratic functions will be the widest?

Example Question #41 : Quadratic Functions

Example Question #45 : Quadratic Functions

Example Question #1 : Circle Functions

Example Question #972 : Algebra Ii

Example Question #973 : Algebra Ii

Example Question #1 : Circle Functions

Example Question #3 : Circle Functions

Example Question #52 : Quadratic Functions

Example Question #5 : Circle Functions

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: