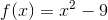From the vertex, we know that the equation of the parabola will take the form for some  .

To calculate that , we plug in the values from the other point we are given, , and solve for :

Now the equation is . This is not an answer choice, so we need to rewrite it in some way.

Expand the squared term:

Distribute the fraction through the parentheses:

Combine like terms:

To find the max or min of , use the vertex formula and substitute the appropriate coefficients.

Since the leading coefficient of  is negative, the parabola opens down, which indicates that there will be a maximum.

The answer is:  

To simplify , determine the factors of the first and last term.

The factor possibilities of :

The factor possibilities of :

Determine the signs.  Since there is a positive ending term and a negative middle term, the signs of the binomials must be both negative.  Write the pair of parenthesis.

These factors must be manipulated by trial and error to determine the middle term.

The correct selection is .

The  answer is . 

Multiply the two through the binomial.

Now that this is in the order of the polynomial , we can use the vertex formula.

Substitute the known coefficients.

The answer is:  

The polynomial is written in the form of:  

This is the standard form for a parabola.

Write the vertex formula, and substitute the known values:

The vertex is at:  

Since the coefficient of  is negative, the curve will open downward, and will have a maximum.

The answer is:  

General parabola equation:

Vertex formula:

Where is the value at the vertex.

Combining equations:

Plugging in values for vertex:

Solving for :

Returning to:

combining equations:

Plugging in values of given intercept:

Solving for

Plugging in value:

Plugging in values for the vertex:

Final equation:

A parabola is a curve that can be represented by a quadratic equation.  The only quadratic here is represented by the function , while the others represent straight lines, circles, and other curves.

It is not necessary to FOIL the binomial in order to solve for the vertex.  Switch the terms of the quantity , and this equation will be in vertex form:

Set the inner quantity equal to zero.

Subtract three on both sides.

Divide by negative two on both sides.

The location of the vertex is at .

To determine the point, substitute the value  back to the original equation.

The point of the vertex is at:   

Since this parabola opens upward, the point of the vertex will be a minimum.

The answer is:  

Write the vertex formula.

The given equation is already in standard polynomial form.

Substitute the known values into the formula.

Substitute this value back into the original equation to determine the y value.

Simplify this expression.

The vertex is located at:  

A parabola is a curve that is represented by a quadratic function. In this case, the only answer that qualifies is .  The other answers represent straight lines, and other types of curves.