All SAT II Math I Resources
Example Questions
Example Question #14 : Simplifying Expressions
Exponentiate:
The difference of two terms can be cubed using the pattern
Where 
Example Question #124 : Single Variable Algebra
How many of the following are prime factors of 
I)
II)
III)
IV)
Three
None
Two
One
Four
Three
Factor 



Therefore, of the given four choices, only 
Example Question #4 : How To Find The Solution Of A Rational Equation With A Binomial Denominator
For all values 
First, factor the numerator. We need factors that multiply to 

We can plug the factored terms into the original expression.
Note that 
This is our final answer.
Example Question #16 : Simplifying Expressions
Simplify the following expression:
When simplifying an equation,you must find a common factor for all values in the equation, including both sides.




This leaves you with

Example Question #21 : Simplifying Expressions
Simplify the expression
Already in simplest form
Simplify the numerator by multiplying in the 
Cancel out like terms in the numerator and denominator.
Example Question #22 : Simplifying Expressions
Simplify:
Rewrite the denominator of the second fraction using a power.
Using the subtraction rule of exponents, we can simplify this as one term.
The expression becomes:
Apply the addition rule of exponents.
The answer is:
Example Question #23 : Simplifying Expressions
Factor an 
We can now cancel out 
Example Question #1 : Functions And Graphs
Define 
Give the range of 
The radicand within a square root symbol must be nonnegative, so
This happens if and only if 

![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218954/gif.latex)


![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218957/gif.latex)


Similarly, 

![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218963/gif.latex)


Therefore, the range of 
![[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218969/gif.latex)
Example Question #2 : Functions And Graphs
Define 
Give the domain of 
The radicand within a square root symbol must be nonnegative, so
This happens if and only if 

![[-4,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218946/gif.latex)
Example Question #1 : Range And Domain
Define the functions 

Give the natural domain of the composite function 
The set of all real numbers
The set of all real numbers
The natural domain of the composite function 
One set is the natural domain of 

The other set is the set of all values of 





Therefore, the other set is the set of all 
Substitute:
This holds for all real numbers, so this set is also the set of all real numbers.
The natural domain of 
All SAT II Math I Resources



















![=\left ( 9y^{2} + 1 \right )\left [ \left (3y \right ) ^{2} - 1^{2} \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/211029/gif.latex)



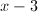
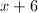






































![(-\infty, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218898/gif.latex)
![[-25,25]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218896/gif.latex)
![[-5,5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218894/gif.latex)
![[0, 25]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218893/gif.latex)
![[0, 5]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218892/gif.latex)






![[-4,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218872/gif.latex)
![(-\infty, 4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218875/gif.latex)
![[0, 4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/218873/gif.latex)


















