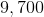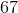SAT II Math I : SAT Subject Test in Math I
Study concepts, example questions & explanations for SAT II Math I
All SAT II Math I Resources
Example Questions
Example Question #4 : Probability
Joe has five apples, four oranges, six bananas, and five limes. What's the probability he gets two apples without replacement?
Since we are trying to get two apples without replacement, this is a condition we need to meet. This means we need to multiply probabilities. For his first pick he has five apples out of twenty fruits in which the probability is 
Example Question #5 : Probability
I pick a number from 
Prime numbers are numbers with factors of 
Answer is 
Example Question #4 : Probability
Sheila flips a coin 
To not get any heads, this would mean Sheila would need to get tails on all the flips. Since there are two choices in a flip and Sheila only want tails, our chances is 
Example Question #11 : Probability
If you draw an ace from and deck then place it back in the deck, what is the probability of drawing another ace?
Since the first card was placed back into the deck, it will have no effect on the second draw.
Since there are 
Example Question #11 : Probability
A fair 6 sided die is rolled twice. What is the probability of observing a 6 both times?
The probability of rolling a 6 once is 
The probability of two independent events happening can be multiplied together. The probability of getting 2 6's is:
Example Question #812 : Sat Subject Test In Math I
If an integer 
Probability is defined as specified outcomes divided by total possible outcomes.
Recall that a prime numbered is defined as a number that is divisible only by one and itself, and 
Notice that the range of values, 
Example Question #1 : Representing Data
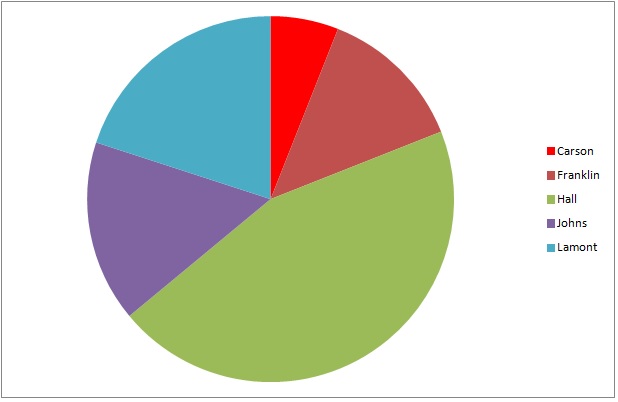
The above graph represents the results of the student body election at Big State College.
Who finished fourth?
Hall
Carson
Lamont
Franklin
Johns
Franklin
The wedges, in descending order of size, are the ones that are green, blue, purple, dull red, and bright red. The dull red wedge, which, according to the legend, represents Franklin, is the fourth-largest.
Example Question #2 : Representing Data
The above graph represents the results of a general election for two seats on the city council of Wilson City. Franklin and Hall are Democrats; Johns and Lamont are Republicans; Carson is an independent.
5,310 people voted for Democrats. Which of the following is the best estimate of the number of people who voted in the election overall?
The two wedges that represent the Democratic candidates - green (Hall) and deep red (Franklin) - make up about 55% of the circle. The problem becomes, essentially, to figure out what 5,310 is 55% of. This can be done by dividing 5,310 by 0.55:
9,700 is the best estimate.
Example Question #1 : Other Data Analyses
Above is the stem-and-leaf display for a group of test scores. Which of the following scores would come closest to being at the 70th percentile?
The stem-and-leaf display represents 53 scores. The score at the 70th percentile would be the score that is greater than 70% of the 53 scores, or
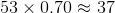
We count up 38 scores from the bottom:
The 38th-lowest score is 78, which is the correct choice.
Certified Tutor
All SAT II Math I Resources
