To determine the domain of the function, we must find the x-values that would give us an undefined result when we plug them into the function. On the numerator, we know that the natural log function can never equal zero or be negative. In the denominator, we can never have a zero. With these conditions in mind, we must now find the x values that makes these undefined situations occur.

For the numerator:

 and 

For the denominator:

Now that we know where x cannot be, we can now write the domain, making sure to use round brackets for the endpoints of the intervals:

The domain refers to all the possible x-values that can be existent on the given function.  Do not confuse this with the range, since this represents all the existent y-values on the graph.

Since there are no discontinuities for any x-value that we may substitute, the domain is all real numbers.

The answer is:  

To find the y-intercept of any line, we must get the equation into the form

where m is the slope and b is the y-intercept.

To manipulate our equation into this form, we must solve for y. First, we must move the x term to the right side of our equation by subtracting it from both sides.

To isolate y, we now must divide each side by 3.

Now that our equation is in the desired form, our y-intercept is simply

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting  for :

Recall that the general form of the quadratic formula is:

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

Simplifying, you get:

Using a calculator, you will get:

 and 

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting  for :

Recall that the general form of the quadratic formula is:

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

Simplifying, you get:

Using a calculator, you will get:

 and 

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting  for . Then, we need to get it into standard form:

Recall that the general form of the quadratic formula is:

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

Simplifying, you get:

Using a calculator, you will get:

 and 

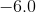
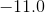
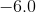
There are two ways to solve this. First, you could substitute in  for :

Take the square-root of both sides and get:

Therefore, your two answers are  and .

You also could have done this by noticing that the problem is a circle of radius , shifted upward by .

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting  for . Then, we need to get it into standard form:

Recall that the general form of the quadratic formula is:

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

Simplifying, you get:

Using a calculator, you will get:

 and 

The easiest way to solve for this kind of simple -intercept is to set  equal to .  You can then solve for the  value in order to find the relevant intercept.

Solve for :

Divide both sides by 40:

To find the x-intercept, you must plug  in for .  

This gives you,

 and you must solve for .  

First, add  to both sides which gives you, 

.  

Then divide both sides by  to get, 

.