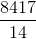Factor out 7 from the numerator:

This simplifies to 7.

If 10 pizzas cost x dollars, then each pizza costs x/10. Similarly, each soda costs y/6. We can add the pizzas and sodas together by finding a common denominator:

Since the values in the pie charts are currently in terms of percentages (/100), we must convert them to degrees (/360, since within a circle) to solve the question. The "5 to 9 years" portion for the financial and construction industries are 18 and 25 percent, respectively. As such, we can cross-multiply both:

18/100 = x/360 

x = 65 degrees

25/100 = y/360

y = 90 degrees

Subtract: 90 – 65 = 25 degrees

Alternatively, we could first subtract the percentages (25 – 18 = 7), then convert the 7% to degree form via the same method of cross-multiplication.

When there are 6 people playing, each contestant has a 1/6 chance of winning.  After the disqualification, the remaining contestants have a 1/5 chance of winning.

1/5 – 1/6 = 6/30 – 5/30 = 1/30.

Begin by simplifying the numerator.

 has a common denominator of .  Therefore, we can rewrite it as:

Now, in our original problem this is really is:

When you divide by a fraction, you really multiply by the reciprocal:

Begin by simplifying the numerator and the denominator.

Numerator

 has a common denominator of .  Therefore, we have:

Denominator

 has a common denominator of .  Therefore, we have:

Now, reconstructing our fraction, we have:

To make this division work, you multiply the numerator by the reciprocal of the denominator:

Recall that dividing is equivalent multiplying by the reciprocal.  Therefore, ((x - 4) / (1 / 2)) / (1 / (x + 4)) = ((x - 4) * 2)  *  (x + 4) / 1. 

Let's simplify this further:

(2x – 8) * (x + 4) = 2x² – 8x + 8x – 32 = 2x² – 32

Begin by isolating the variables:

Now, the common denominator of the variable terms is . The common denominator of the constant values is . Thus, you can rewrite your equation:

Simplify:

Cross-multiply:

Simplify:

Finally, solve for :

A negative exponent in the numerator of a fraction can be rewritten with a positive exponent in the denominator. The same is true for a negative exponent in the denominator. Thus, .

When is multiplied by , the numerators and denominators cancel out, and you are left with 1.

Another way to represent this question is:

In the one's column, and add to produce a number with a two in the one's place. In the ten's column, we can see that a one must carry in order to get a digit in the hundred's place. Together, we can combine these deductions to see that the sum of and must be twelve (a one in the ten's place and a two in the one's place).

In the one's column:

The one carries to the ten's column.

In the ten's column:

The three goes into the answer and the one carries to the hundred's place. The final answer is 132. From this, we can see that because .

Using this information, we can solve for .

You can check your answer by returning to the original addition and plugging in the values of and .