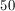PSAT Math : PSAT Mathematics
Study concepts, example questions & explanations for PSAT Math
All PSAT Math Resources
Example Questions
Example Question #1321 : Psat Mathematics
Solve for 
First distribute the fractions:
Combine like terms:
Example Question #1322 : Psat Mathematics
Solve for 
First distribute to eliminate the parentheses:
Then combine like terms:
Example Question #1323 : Psat Mathematics
x = 1/2
What does 1/x + 1/(x + 4) equal?
4
4/9
20/9
9/2
20
20/9
1/x + 1/(x+4) =
1/(1/2) + 1/ (1/2 + 4) =
1/ (1/2) + 1 / (9/2) =
2 + 2/9
20/9
Example Question #1 : How To Solve For A Variable As Part Of A Fraction
Solve for 
Cross multiply.
Dsitribute.
Solve for 
Example Question #1324 : Psat Mathematics
If 
To solve this question, substitute -5 in for x in the numerator and denominator. Remember that the square of a negative number is positive.
45 / -9 = -5
Example Question #4 : How To Solve For A Variable As Part Of A Fraction
If 
none of these
38/3
7/12
3/38
9/114
38/3
cross multiply:
(6)(19) = 9x
114=9x
x = 38/3
Example Question #2 : How To Solve For A Variable As Part Of A Fraction
Find x.
None
Cross multiply:
Example Question #2 : How To Solve For A Variable As Part Of A Fraction
The numerator of a fraction is the sum of 4 and 5 times the denominator. If you divide the fraction by 2, the numerator is 3 times the denominator. Find the simplified version of the fraction.
Let numerator = N and denominator = D.
According to the first statement,
N = (D x 5) + 4.
According to the second statement, N / 2 = 3 * D.
Let's multiply the second equation by –2 and add itthe first equation:
–N = –6D
+[N = (D x 5) + 4]
=
–6D + (D x 5) + 4 = 0
–1D + 4 = 0
D = 4
Thus, N = 24.
Therefore, N/D = 24/4 = 6.
Example Question #81 : Algebraic Fractions
Solve for 
Solve for 
Step 1: Cross-multiply to eliminate the fraction
Step 2: Solve for 
Example Question #1 : Data Analysis
This semester, Mary had five quizzes that were each worth 10% of her grade. She scored 89, 74, 84, 92, and 90 on those five quizzes. Mary also scored a 92 on her midterm that was worth 25% of her grade, and a 91 on her final that was also worth 25% of her class grade. What was Mary's final grade in the class?
89
93
87
85
91
89
To find her average grade for the class, we need to multiply Mary's test scores by their corresponding weights and then add them up.
The five quizzes were each worth 10%, or 0.1, of her grade, and the midterm and final were both worth 25%, or 0.25.
average = (0.1 * 89) + (0.1 * 74) + (0.1 * 84) + (0.1 * 92) + (0.1 * 90) + (0.25 * 92) + (0.25 * 91) = 88.95 = 89.
Looking at the answer choices, they are all spaced 2 percentage points apart, so clearly the closest answer choice to 88.95 is 89.
Certified Tutor
Certified Tutor
All PSAT Math Resources
