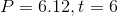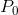Math Modeling : Intro to Probability Models
Study concepts, example questions & explanations for Math Modeling
All Math Modeling Resources
Example Questions
Example Question #1 : Probability Models
A beauty supply company manufactures a variety of brushes. Quality control engineers work to ensure that the defected brushes in the factory will be detected prior to shipping them. It is estimated that approximately 0.2% of the brushes made will be defected. Tests can be done individually on the brushes or on batches of the brushes. If the test on a batch of brushes fails, it means that one or more of the brushes in that particular batch are defected. The estimated cost is 4 cents for a single brush, and 
By testing brush batches in groups of 12 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 10 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 20 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 9 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 15 will reduce testing costs without sacrificing the quality.
By testing brush batches in groups of 15 will reduce testing costs without sacrificing the quality.
First identify the known variables and assumptions.
If
If a batch of brushes is tested and if the test shows that all the brushes are good then,
If the batch test shows that there is a defected brush in the batch then,
Use a discrete probability model to find the most cost-effected quality control procedure for detecting defected brushes.
Consider the random variable
that has a probability of
If the probability of a brush being good is 
Now there are 
Therefore the expected value of the random variable 
Therefore the average testing cost is,
Using the law of large numbers minimizing 
Now answer the question.
By testing brush batches in groups of 15 will reduce testing costs without sacrificing the quality.
Example Question #1 : Probability Models
An oil spill occurs at a factory 12 kilometers up stream from a town. One hour after the spill happens it reaches the stream and a 1600 meters long patch of oil begins to flow towards the town at a rate of 2 kilometers per hour. The maximum concentration of the oil in the water is 15 times the acceptable level. What is the maximum concentration expected in town and when will it arrive?
Identify what is known and the assumptions.
This is a diffusion problem and thus a diffusion equation will be used with a term of relative concentration.
The relative concentration is denoted as
This function has been normalized resulting in the following.
The law of conservation of mass will also be useful is solving this problem.
The goal is to calculate the maximum pollution level in town.
The diffusion equation is,
Using the Fourier transforms to solve the diffusion equation is as follows.
For this particular function
so the interval will be
Calculate 
Now find where the maximum occurs in time.
All Math Modeling Resources
