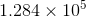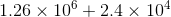To simplify a radical expression, first find the prime factorization of the radicand, which is 120 here.

Pair up like factors, then apply the Product of Radicals Property:

,

the simplest form of the radical.

To simplify a radical expression, first, find the prime factorization of the radicand. First, we will attempt simplify  as follows:

Since no prime factor appears twice, the expression cannot be simplified further. The same holds for , since .

It follows that the expression  is already in simplest form.

First, rewrite each radical expression using rational exponents:

Multiply these expressions using the Product of Powers Property:

This can be rewritten in radical form as .

Apply the properties of exponents to the expression as follows:

By the Power of a Power Property:

Restating:

By the Product of Powers of Property:

,

the correct response.

You can solve this problem in several ways. One way is to convert each number out of scientific notation and write it out fully, then find the sum of the two values and convert the answer back into scientific notation.

Another, potentially faster, way to solve this problem is to convert one answer into the same scientific-notational terms as the other and then sum them.

Convert 7,200,000 to scientific notation as follows:

Move the (implied) decimal point until it is immediately after the first nonzero digit (the 7). This required moving the point six units to the left:

It follows that 7,200,000 can be rewritten as .

By similar reasoning, 5,000,000 can be rewritten as .

Thus,

Rearrange and regroup the expressions so that the powers of ten are together:

Multiply the numbers in front. Also, multiply the powers of ten by adding exponents:

In order for the number to be in scientific notation, the number in front must be between 1 and 10. An adjustment must be made by moving the implied decimal point in 36 one unit left. It follows that

Therefore,

,

the correct response.

Scientific notation refers to a number expressed in the form

,

where and is an integer.

Each factor can be rewritten in scientific notation as follows:

Now, substitute:

Apply the Product of Powers Property:

This is in scientific notation and is the correct choice.

Each term in the sequence is generated from the previous term by adding 6,as follows:

The correct response is 48. This is confirmed by adding 6 again:

Each term after the first is generated from the previous term by incrementing; the increment begins with 4 and increases by 2 with each term generated. Observe:

,

the correct response. This is confirmed by adding 16 to this term:

The second and third terms are generated by adding, then multiplying by, 1, respectively:

This is repeated for each subsequent pair of terms, except that the number is increased by 1 for each pair:

,

the correct response. This can be confirmed by adding 5 to this term:

.