All HiSET: Math Resources
Example Questions
Example Question #1 : Understand And Apply Concepts Of Equations
Give the nature of the solution set of the equation

Two rational solutions
One rational solution
Two imaginary solutions
One imaginary solution
Two irrational solutions
Two imaginary solutions
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
This can be done by simply switching the first and second terms:
The key to determining the nature of the solution set is to examine the discriminant 

The discriminant has a negative value. It follows that the solution set comprises two imaginary values.
Example Question #18 : Algebraic Concepts
Give the nature of the solution set of the equation
Two irrational solutions
One rational solution
One imaginary solution
Two rational solutions
Two imaginary solutions
Two imaginary solutions
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
This can be done by adding 17 to both sides:
The key to determining the nature of the solution set is to examine the discriminant


This value is negative. Consequently, the solution set comprises two imaginary numbers.
Example Question #19 : Algebraic Concepts
Give the nature of the solution set of the equation
Two rational solutions
Two imaginary solutions
One rational solution
One imaginary solution
Two irrational solutions
Two irrational solutions
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
To accomplish this, first, multiply the binomials on the left using the FOIL technique:
Collect like terms:
Now, subtract 18 from both sides:
The key to determining the nature of the solution set is to examine the discriminant 

The discriminant is a positive number, so there are two real solutions. Since 73 is not a perfect square, the solutions are irrational.
Example Question #1 : Quadratic Equations
Give the nature of the solution set of the equation
Two imaginary solutions
One imaginary solution
One rational solution
Two irrational solutions
Two rational solutions
Two imaginary solutions
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
To accomplish this, first, multiply the binomials on the left using the FOIL technique:
Collect like terms:
Now, add 18 to both sides:
The key to determining the nature of the solution set is to examine the discriminant 

This discriminant is negative. Consequently, the solution set comprises two imaginary numbers.
Example Question #2 : Quadratic Equations
Give the nature of the solution set of the equation
One imaginary solution
Two imaginary solutions
Two rational solutions
One rational solution
Two irrational solutions
Two irrational solutions
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
This can be done by switching the first and third terms on the left:
The key to determining the nature of the solution set is to examine the discriminant



The discriminant is a positive number but not a perfect square. Therefore, there are two irrational solutions.
Example Question #11 : Understand And Apply Concepts Of Equations
Give the nature of the solution set of the equation
Two imaginary solutions
Two rational solutions
Two irrational solutions
One rational solution
One imaginary solution
Two irrational solutions
To determine the nature of the solution set of a quadratic equation, it is necessary to first express it in standard form
This can be done by subtracting 34 from to both sides:
The key to determining the nature of the solution set is to examine the discriminant



The discriminant is a positive number but not a perfect square. Therefore, there are two irrational solutions.
Example Question #1 : Rational And Radical Equations
Solve the following equation:
The first step to solving an equation where 
![\sqrt[3]{5-2x}=-1](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072124/gif.latex)
Now that the radical is isolated, clear the radical by raising both sides to the power of 3. Note:
Now we want to isolate the 
Finally, divide both sides by 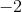

Example Question #1 : Rearrange Formulas/Equations To Highlight A Quantity Of Interest
Solve for 
To solve for 

Multiply both sides by 
Subtract 
Multiply both sides by 

the correct response.
Example Question #2 : Rearrange Formulas/Equations To Highlight A Quantity Of Interest
Solve for 
Assume 
To solve for 

Subtract 
Divide both sides by 9:
Take the square root of both sides:
Simplify the expression on the right by splitting it, and taking the square root of numerator and denominator:

the correct response.
Example Question #241 : Hi Set: High School Equivalency Test: Math
Solve for 
To solve for 

First, take the reciprocal of both sides:
Multiply both sides by 
Distribute on the right:
Subtract 1 from both sides, rewriting 1 as 

the correct response.
Certified Tutor
Certified Tutor
All HiSET: Math Resources


































![\sqrt[3]{5-2x}+5=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072122/gif.latex)

![x=\sqrt[3]{5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072121/gif.latex)

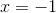
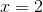
![\sqrt[3]{5-2x}+5=4](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1072123/gif.latex)
![\sqrt[3]{5-2x}+5-5=4-5](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1082121/gif.latex)

![(\sqrt[3]{5-2x})^3=(-1)^3](http://cdn-s3.varsitytutors.com/uploads/formula_image/image/1082123/gif.latex)















































