All High School Math Resources
Example Questions
Example Question #11 : Isosceles Triangles
An isoceles triangle has a base angle that is twice the vertex angle. What is the sum of the base and vertex angles?
All triangles have 
Let 

So the equation to solve becomes:

Thus 

The sum of the vertex and one base angle is 
Example Question #12 : Isosceles Triangles
An isoceles triangle has a vertex angle that is 
Every triangle has 
Let 

So the equation to solve becomes 

Thus the base angles are 

Example Question #281 : Geometry
An isoceles triangle has a base angle that is 
Every triangle has 180 degrees. An isoceles triangle has one vertex angle and two congruent base angles.
Let 

Then the equation to solve becomes:


Then the vertex angle is 


Example Question #11 : Triangles
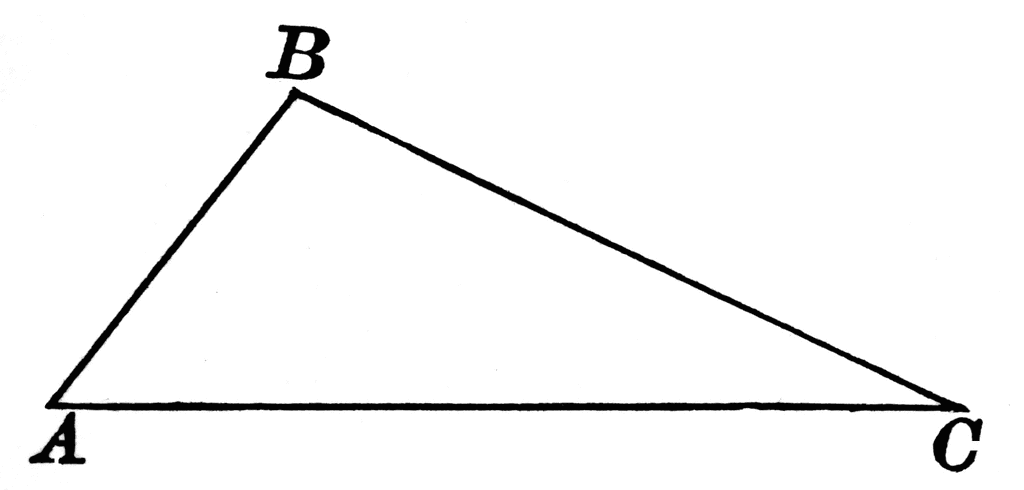
In triangle ABC, Angle A = x degrees, Angle B = 2x degrees, and Angle C = 3x+30 degrees. How many degrees is Angle B?
45°
30°
105°
25°
50°
50°
Because the interior angles of a triangle add up to 180°, we can create an equation using the variables given in the problem: x+2x+(3x+30)=180. This simplifies to 6X+30=180. When we subtract 30 from both sides, we get 6x=150. Then, when we divide both sides by 6, we get x=25. Because Angle B=2x degrees, we multiply 25 times 2. Thus, Angle B is equal to 50°. If you got an answer of 25, you may have forgotten to multiply by 2. If you got 105, you may have found Angle C instead of Angle B.
Example Question #12 : Triangles
An isosceles triangle has a base angle that is six more than three times the vertex angle. What is the base angle?
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Let 

Then the equation to solve becomes
or

Solving for 
Example Question #221 : Act Math
The base angle of an isosceles triangle is thirteen more than three times the vertex angle. What is the difference between the vertex angle and the base angle?
Every triangle has 
Let 

The equation to solve becomes 
Now we can solve for the vertex angle.
The difference between the vertex angle and the base angle is 
Example Question #11 : Triangles
An isoceles triangle has a base angle that is five less than twice the vertex angle. What is the sum of the base and vertex angles?
Each triangle has 
An isoceles triangle has two congruent base angles and one vertex angle.
Let 

Then the equation to solve becomes 

Add 

Divide both sides by 



Example Question #281 : Geometry
An isoceles triangle has a base angle that is twice the vertex angle. What is the sum of one base angle and the vertex angle?
Every triangle contains 
Let 

So the equation to solve becomes 




Example Question #13 : Triangles
A triangle has a perimeter of 


The answer is 
Since we know that the permieter is 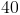


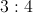





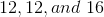

Example Question #20 : Isosceles Triangles
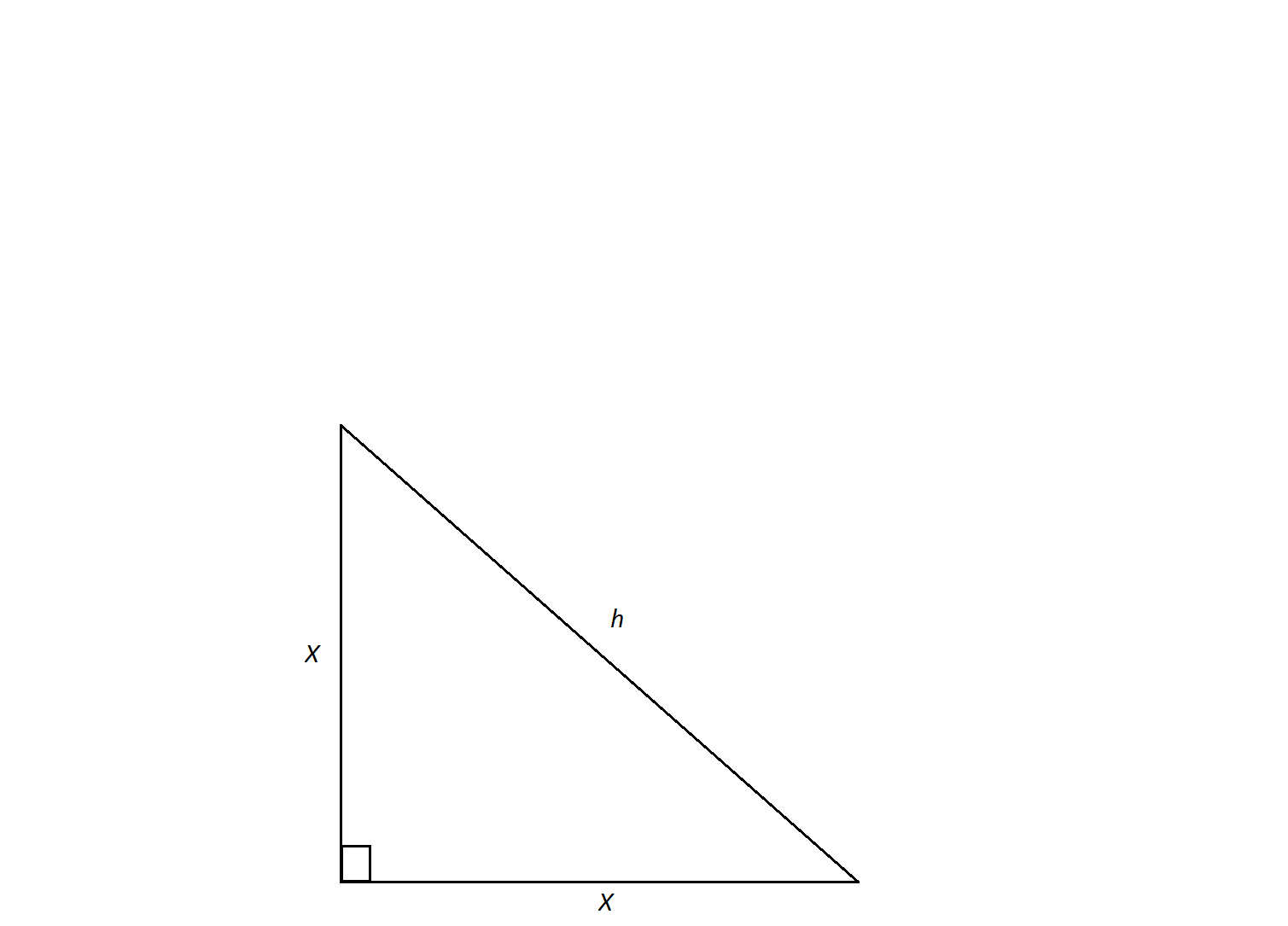
In an isosceles right triangle, two sides equal 

This problem represents the definition of the side lengths of an isosceles right triangle. By definition the sides equal 



All High School Math Resources





























































