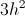All High School Math Resources
Example Questions
Example Question #111 : Plane Geometry
If the average (arithmetic mean) of two noncongruent angles of an isosceles triangle is 
Since the triangle is isosceles, we know that 2 of the angles (that sum up to 180) must be equal. The question states that the noncongruent angles average 55°, thus providing us with a system of two equations:
Solving for x and y by substitution, we get x = 70° and y = 40° (which average out to 55°).
70 + 70 + 40 equals 180 also checks out.
Since 70° is not an answer choice for us, we know that the 40° must be one of the angles.
Example Question #4 : Acute / Obtuse Triangles
Points A, B, and C are collinear (they lie along the same line). The measure of angle CAD is 


Find the measure of 
The measure of 








Because the measures of the three angles in a triangle must add up to 





Example Question #141 : Triangles
The base angle of an isosceles triangle is 
Every triangle has 180 degrees. An isosceles triangle has one vertex angle and two congruent base angles.
Solve the equation 
x = 180 - 27 - 27
x = 126
Therefore the measure of the vertex angle is 
Example Question #11 : Isosceles Triangles
An isosceles triangle has an area of 12. If the ratio of the base to the height is 3:2, what is the length of the two equal sides?
6
5
3√3
4√3
4
5
Area of a triangle is ½ x base x height. Since base:height = 3:2, base = 1.5 height. Area = 12 = ½ x 1.5 height x height or 24/1.5 = height2. Height = 4. Base = 1.5 height = 6. Half the base and the height form the legs of a right triangle, with an equal leg of the isosceles triangle as the hypotenuse. This is a 3-4-5 right triangle.

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Isosceles Triangle
Two sides of a triangle each have length 6. All of the following could be the length of the third side EXCEPT
This question is about the Triangle Inequality, which states that in a triangle with two sides A and B, the third side must be greater than the absolute value of the difference between A and B and smaller than the sum of A and B.
Applying the Triangle Inequality to this problem, we see that the third side must be greater than the absolute value of the difference between the other two sides, which is |6-6|=0, and smaller than the sum of the two other sides, which is 6+6=12. The only answer choice that does not satisfy this range of possible values is 12 since the third side must be LESS than 12.
Example Question #1 : How To Find The Area Of An Acute / Obtuse Triangle
Find the area of a triangle whose base is 

This problem is solved using the geometric formula for the area of a triangle.
Convert feet to inches.
Example Question #112 : Triangles
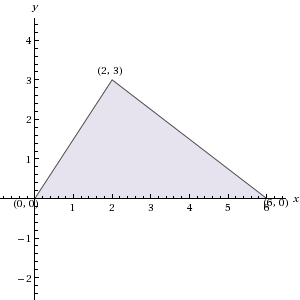
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?
9
20
18
12
10
Example Question #1 : How To Find The Area Of An Acute / Obtuse Triangle
What is the area of a triangle with a height of 

When searching for the area of a triangle we are looking for the amount of the space enclosed by the triangle.
The equation for area of a triangle is
Plug the values for base and height into the equation yielding
Then multiply the numbers together to arrive at the answer 
Example Question #113 : Triangles
The height, 



If 


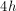
Using the formula for the area of a triangle (


Example Question #187 : Plane Geometry
A triangle has a perimeter of 36 inches, and one side that is 12 inches long. The lengths of the other two sides have a ratio of 3:5. What is the length of the longest side of the triangle?
15
12
14
8
9
15
We know that the perimeter is 36 inches, and one side is 12. This means, the sum of the lengths of the other two sides are 24. The ratio between the two sides is 3:5, giving a total of 8 parts. We divide the remaining length, 24 inches, by 8 giving us 3. This means each part is 3. We multiply this by the ratio and get 9:15, meaning the longest side is 15 inches.
Certified Tutor
Certified Tutor
All High School Math Resources