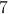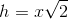Call Now to Set Up Tutoring:

(888) 888-0446

High School Math : Triangles

Study concepts, example questions & explanations for High School Math

Create An Account

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #31 : Triangles

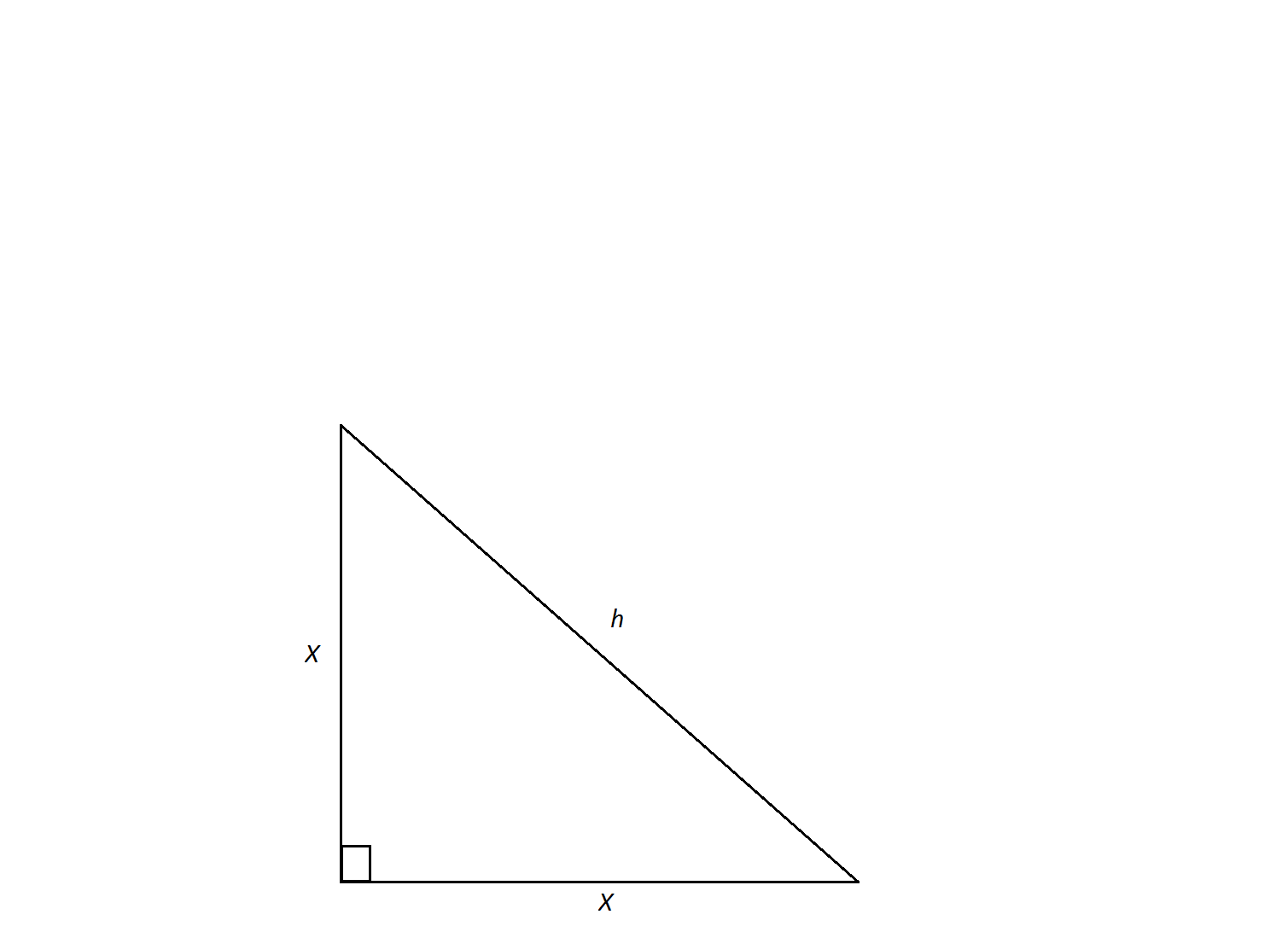
Isosceles

The measure of the sides of this isosceles right triangle are $x=3\sqrt{2}$ . Find the measure of its hypotenuse, .

Possible Answers:

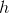
Not enough information to solve

Correct answer:

Explanation:

An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as $45^{\circ}-45^{\circ}-90^{\circ}$ triangles and their side lenghts follow a specific pattern that states you can calculate the length of the hypotenuse of an isoceles triangle by multiplying the length of one of the legs by the square root of 2.

$h=x\sqrt{2}$

$h=3\sqrt{2}*\sqrt{2}$

h=3*2

$\rightarrow6$

Report an Error

Example Question #1 : Acute / Obtuse Triangles

Two similiar triangles have a ratio of perimeters of $7:2$ .

If the smaller triangle has sides of 3, 7, and 5, what is the perimeter of the larger triangle.

Possible Answers:

$49.5$

$50.5$

$51.5$

$52.5$

$48.5$

Correct answer:

$52.5$

Explanation:

Adding the sides gives a perimeter of 15 for the smaller triangle. Multipying by the given ratio of $\frac{7}{2}$ , yields 52.5.

Report an Error

Example Question #2 : Isosceles Triangles

Two sides of an isosceles triangle are 20 and 30. What is the difference of the largest and the smallest possible perimeters?

Possible Answers:

The answer cannot be determined

Correct answer:

Explanation:

The trick here is that we don't know which is the repeated side. Our possible triangles are therefore 20 + 20 + 30 = 70 or 30 + 30 + 20 = 80. The difference is therefore 80 – 70 or 10.

Report an Error

Example Question #1 : Acute / Obtuse Triangles

Two similiar triangles exist where the ratio of perimeters is 4:5 for the smaller to the larger triangle. If the larger triangle has sides of 6, 7, and 12 inches, what is the perimeter, in inches, of the smaller triangle?

Possible Answers:

Correct answer:

Explanation:

The larger triangle has a perimeter of 25 inches. Therefore, using a 4:5 ratio, the smaller triangle's perimeter will be 20 inches.

Report an Error

Example Question #1 : Acute / Obtuse Triangles

If a = 7 and b = 4, which of the following could be the perimeter of the triangle?

Msp30320bea9chb26d18hh0000627i1e4ibba8c4f5

I. 11

II. 15

III. 25

Possible Answers:

I Only

II and III Only

I, II and III

II Only

I and II Only

Correct answer:

II Only

Explanation:

Consider the perimeter of a triangle:

P = a + b + c

Since we know a and b, we can find c.

In I:

11 = 7 + 4 + c

11 = 11 + c

c = 0

Note that if c = 0, the shape is no longer a trial. Thus, we can eliminate I.

In II:

15 = 7 + 4 + c

15 = 11 + c

c = 4.

This is plausible given that the other sides are 7 and 4.

In III:

25 = 7 + 4 + c

25 = 11 + c

c = 14.

It is not possible for one side of a triangle to be greater than the sum of both of the other sides, so eliminate III.

Thus we are left with only II.

Report an Error

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Solve for . (Not drawn to scale).

Possible Answers:

57^o

22^o

81^o

53^o

Correct answer:

53^o

Explanation:

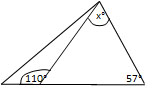
The angles of a triangle must add to 180^o. In the triangle to the right, we know one angle and can find another using supplementary angles.

57+(180-110)+x=180

Now we only need to solve for .

57+70+x=180

x=180-(57+70)=180-127

x=53^o

Report an Error

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

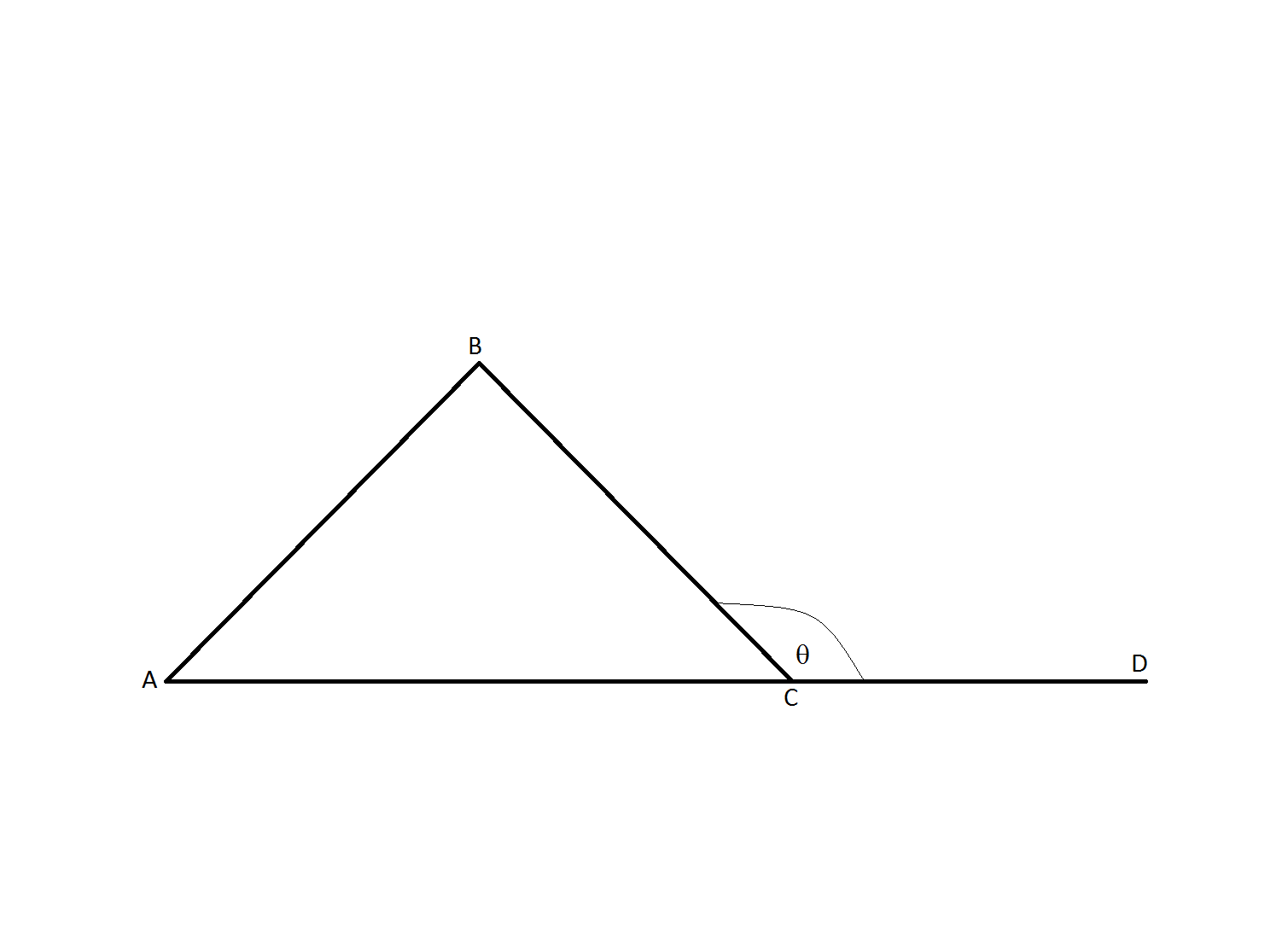Exterior_angle If $\angle A=42^{\circ}$ and $\angle B=76^{\circ}$ , what is the measure of $\theta$ ?

Possible Answers:

$62^{\circ}$

$76^{\circ}$

$118^{\circ}$

$42^{\circ}$

Not enough information to solve

Correct answer:

$118^{\circ}$

Explanation:

All of the interior angles of a triangle add up to $180^{\circ}$ .

If $\angle A=42^{\circ}$ and $\angle B=76^{\circ}$ , then

$\angle C= 180^{\circ}-(42^{\circ}+76^{\circ})$

Therefore, $\angle C=62^{\circ}$

Now, $\theta$ will equal $180^{\circ}-\angle C$ because $\angle C$ and $\theta$ form a straight line. Therefore,

$\theta=180^{\circ}-62^{\circ}$

$\rightarrow118^{\circ}$

Also, by definition, the angle of an exterior angle of a triangle is equal to the measure of the two interior angles opposite of it $\dpi{100} (\theta =76^{\circ}+42^{\circ}\rightarrow 118^{\circ})$ .

Report an Error

Example Question #2 : Acute / Obtuse Triangles

Two interior angles in an obtuse triangle measure $123^{\circ}$ and $11^{\circ}$ . What is the measurement of the third angle.

Possible Answers:

$123^{\circ}$

$46^{\circ}$

$104^{\circ}$

$50^{\circ}$

$57^{\circ}$

Correct answer:

$46^{\circ}$

Explanation:

Interior angles of a triangle always add up to 180 degrees.

Report an Error

Example Question #1 : Acute / Obtuse Triangles

In a given triangle, the angles are in a ratio of 1:3:5. What size is the middle angle?

Possible Answers:

$45^{\circ}$

$60^{\circ}$

$75^{\circ}$

$20^{\circ}$

$90^{\circ}$

Correct answer:

$60^{\circ}$

Explanation:

Since the sum of the angles of a triangle is $180^{\circ}$ , and given that the angles are in a ratio of 1:3:5, let the measure of the smallest angle be , then the following expression could be written:

$x+3x+5x=180$

$9x=180$

$x=20$

If the smallest angle is 20 degrees, then given that the middle angle is in ratio of 1:3, the middle angle would be 3 times as large, or 60 degrees.

Report an Error

Example Question #4 : Isosceles Triangles

Triangle ABC has angle measures as follows:

$\dpi{100} \small m\angle ABC=4x+3$

$\dpi{100} \small m\angle ACB=2x+6$

$\dpi{100} \small m\angle BAC=3x$

What is $\dpi{100} \small m\angle BAC$ ?

Possible Answers:

Correct answer:

Explanation:

The sum of the measures of the angles of a triangle is 180.

Thus we set up the equation $\dpi{100} \small 4x+3+2x+6+3x=180$

After combining like terms and cancelling, we have $\dpi{100} \small 9x=171\rightarrow x=19$

Thus $\dpi{100} \small m\angle BAC=3x=57$

Report an Error

View Tutors

Anthony
Certified Tutor

CUNY New York City College of Technology, Bachelor of Science, Civil Engineering.

View Tutors

Alejandro
Certified Tutor

Kennesaw State University, Bachelor of Science, Computer Software Engineering.

View Tutors

Karen
Certified Tutor

Pontifical Bolivarian University, Bachelor in Arts, Bilingual Education. Pontifical Bolivarian University, Certificate, Bilin...

All High School Math Resources

8 Diagnostic Tests 613 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Dallas Fort Worth, SAT Tutors in Miami, SAT Tutors in Los Angeles, LSAT Tutors in Chicago, LSAT Tutors in Washington DC, MCAT Tutors in Miami, Reading Tutors in San Diego, Biology Tutors in Houston, Physics Tutors in Chicago, GRE Tutors in Denver

Popular Courses & Classes

LSAT Courses & Classes in Washington DC, SAT Courses & Classes in Seattle, ACT Courses & Classes in Boston, SAT Courses & Classes in Miami, SAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Chicago, SSAT Courses & Classes in New York City, SAT Courses & Classes in Washington DC, GRE Courses & Classes in Boston, SSAT Courses & Classes in Seattle

Popular Test Prep

GMAT Test Prep in Washington DC, ACT Test Prep in San Francisco-Bay Area, LSAT Test Prep in Miami, GRE Test Prep in Philadelphia, SSAT Test Prep in Atlanta, MCAT Test Prep in Boston, ISEE Test Prep in Seattle, ISEE Test Prep in Miami, MCAT Test Prep in Denver, SSAT Test Prep in Chicago

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

High School Math : Triangles

Study concepts, example questions & explanations for High School Math

All High School Math Resources

Example Questions

Example Question #31 : Triangles

Example Question #1 : Acute / Obtuse Triangles

Example Question #2 : Isosceles Triangles

Example Question #1 : Acute / Obtuse Triangles

Example Question #1 : Acute / Obtuse Triangles

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Example Question #1 : How To Find An Angle In An Acute / Obtuse Triangle

Example Question #2 : Acute / Obtuse Triangles

Example Question #1 : Acute / Obtuse Triangles

Example Question #4 : Isosceles Triangles

All High School Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: