The length of a side of a square is equal to the square root of its area. Square 1 has area 16, so each side has length .

The length of a side of a square is one fourth its perimeter. Square 2 has perimeter 16, so each side has length .

The squares are of equal size, so the correct response is "neither".

To find the area, you need to multiply the dimensions. First, however, we need to find our width.

We can find our width by using the clue: "...one and a half times the length"

So, do the following:

Next, perform the following operation:

Making our answer:

Recall the relationship between a central angle and the length of the arc that it intercepts.

Since the radius of the circle is given, we can find its circumference.

For the given circle,

We can plug in all the given information and solve for the central angle then.

Drawing out the rectangle in question shows that we can use the Pythagorean Theorem to find the width of the rectangle.

Now, recall how to find the area of a rectangle:

Plug in the width and height of the rectangle to find the area.

In order to find the area of the shaded region, we will need to find the area of the circle then subtract the area of the square from it.

Start by finding the area of the square. Since we know the side length of the square, we can write the following:

Next, we find the area of the circle. Since the question states that the length of a side of the square is half the radius of the circle, the radius of the circle must be . Thus, we can find the area of the circle.

Now, subtract these two values to find the area of the shaded region.

Figuring out the perimeter of a square from this information is luckily pretty easy. Since the sides of a square are all the same size, you know also that .

Taking the square root of both sides, you get:

Now, the perimeter of the square is just , or .

Since the four sides of a square are equal, you know that the perimeter of a square is defined as:

For our data, this is:

Solving for , you get:

Now, the area of a square is just:

 or , which is the same as .

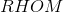
The figure referenced is below.

The sides of a rhombus are congruent by definition, so , making  isosceles (and possibly equilateral).

Also, consecutive angles of a rhombus are supplementary, as they are with all parallelograms, so

.

, having measure greater than , is obtuse, making  an obtuse triangle. Also, the triangle is not equilateral, since such a triangle must have three  angles.

The correct response is that  is obtuse and isosceles, but not equilateral.

Statement I asserts that two pairs of consecutive angles are congruent. This does not prove that the figure is a parallelogram. For example, an isosceles trapezoid has two pairs of congruent base angles, which are consecutive. 

Statement II asserts that both pairs of opposite angles are congruent. By a theorem of geometry, this proves the quadrilateral to be a parallelogram.

Statement III asserts that two pairs of consecutive angles are supplementary. While all parallelograms have this characteristic, trapezoids do as well, so this does not prove the figure a parallelogram.

The correct response is Statement II only.

A rectangle is defined as a parallelogram with four right, or , angles.

Since opposite angles of a paralellogram are congruent, if one angle measures , so does its opposite. Since consecutive angles of a paralellogram are supplementary - that is, their degree measures total  - if one angle measures , then both of the neighboring angles measure .

In short, in a parallelogram, if one angle is right, all are right and the parallelogram is a rectangle. All three statements assert that one angle is right, so from any one, it follows that the figure is a rectangle. The correct response is Statements I, II, or III.

Note that the sidelengths are irrelevant.