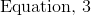All Common Core: 8th Grade Math Resources
Example Questions
Example Question #11 : Functions
Select the table that properly represents a function.





Each of the tables provided contains sets of ordered pairs. The input column represents the x-variables, and the output column represents the y-variables. We can tell if a set of ordered pairs represents a function when we match x-values to y-values.
In order for a table to represents a function, there must be one and only one input for every output. This means that our correct answer will have all unique input values:

Functions cannot have more than one input value that is the same; thus, the following tables do not represent a function:



Example Question #1 : Compare Properties Of Two Functions: Ccss.Math.Content.8.F.A.2
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
Example Question #261 : Grade 8
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
Example Question #262 : Grade 8
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
Example Question #2 : Compare Properties Of Two Functions: Ccss.Math.Content.8.F.A.2
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
Example Question #261 : Grade 8
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
Example Question #6 : Compare Properties Of Two Functions: Ccss.Math.Content.8.F.A.2
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
Example Question #7 : Compare Properties Of Two Functions: Ccss.Math.Content.8.F.A.2
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
Example Question #8 : Compare Properties Of Two Functions: Ccss.Math.Content.8.F.A.2
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
Example Question #9 : Compare Properties Of Two Functions: Ccss.Math.Content.8.F.A.2
The table and the equation provided represent two different functions. Which of these two functions—either table or equation form—has the greater rate of change, and what is the rate of change?

The rate of change is also known as the slope. As we have learned we can use the following equation to solve for the slope of the table:
An input/output table displays sets of ordered pairs. The input column represents the x-values and the output column represents the y-values. We can select two sets of ordered pairs from the table to solve for the slope:
The slope for our table is
In order to determine the slope of the equation, we need to make sure the equation is in slope-intercept form:
In this equation, the variables 


The given formula for this problem was provided in slope-intercept form; thus, the slope for the equation is
The function with the greatest rate of change will possess the greatest slope. In this case, the greater slope is 
All Common Core: 8th Grade Math Resources