AP Calculus AB : Concept of the Derivative
Study concepts, example questions & explanations for AP Calculus AB
All AP Calculus AB Resources
Example Questions
Example Question #112 : Ap Calculus Ab
The function is differentiable at the point . List which of the following statements must be true about :
1) The limit exists.
_________________________________________________________
2)
_________________________________________________________
3)
_________________________________________________________
4)
_________________________________________________________
5)
1, and 5
1, 2, and 4
1,3,4,and 5
1, 3, and 5
All must be true.
1, 2, and 4
1) If a function is differentiable, then by definition of differentiability the limit defined by,
exists. Therefore (1) is required by definition of differentiability. _______________________________________________________________
2) If a function is differentiable at a point then it must also be continuous at that point. (This is not conversely true).
For a function to be continuous at a point we must have:
Therefore (2) and (4) are required.
-----------------------------------------------------------------------------------------
3)
This is not required, the left side of the equation is the definition of a derivative at a point for a function . The derivative at a point does not have to equal to the function value at that point, it is equal to the slope at that point. Therefore 3 does not have to be true.
However, we can note that it is possible for a function and its' derivative to be equal for a given point. Sine and cosine, for instance will intersect periodically. Another example would be the exponential function which has itself as its' derivative .
______________________________________________________________
4) See 2
_______________________________________________________________
5)
Again, the function does not have to approach the same limit as its' derivative. It is possible for a function to behave in this manner, such as in the case of sine and its' derivative cosine, which will both have the same limit at points where they intersect.
Example Question #113 : Ap Calculus Ab
When the limit fails to exist,
The function is not differentiable at .
The function is not defined at .
The function is not continuous at .
None of the above necessarily
The function is not differentiable at .
By definition of differentiability, when the limit exists. When exists, we say the function is 'differentiable at '.
Example Question #114 : Ap Calculus Ab
Which of the following functions is differentiable at , but not continuous there?
They are all differentiable and continuous at
They are all differentiable and continuous at
All of the functions are differentiable at . If you examine the graph of each of the functions, they are all defined at , and do not have a corner, cusp, or a jump there; they are all smooth and connected (Not necessarily everywhere, just at ). Additionally it is not possible to have a function that is differentiable at a point, but not continuous at that same point; differentiablity implies continuity.
Example Question #115 : Ap Calculus Ab
For which of the following functions does a limit exist at , but not a y-value?
To answer the question, we must find an equation which satisfies two criteria:
(1) it must have limits on either side of that approach the same value and (2) it must have a hole at .
Each of the possible answers provide situations which demonstrate each combination of (1) and (2). That is to say, some of the equations include both a limit and a y-value at , neither, or,in the case of the piecewise function, a y-value and a limit that does not exist.
In the function, , the numerator factors to
while the denominator factors to . As a result, the graph of this
function resembles that for , but with a hole at . Therefore, the limit
at exists, even though the y-value is undefined at .
Example Question #11 : Derivatives
What is the derivative of ?
To solve this problem, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
Remember that anything to the zero power is one.
Example Question #5 : General Derivatives And Rules
What is the derivative of ?
To solve this problem, we can use the power rule. That means we lower the exponent of the variable by one and multiply the variable by that original exponent.
We're going to treat as , as anything to the zero power is one.
That means this problem will look like this:
Notice that , as anything times zero is zero.
Remember, anything to the zero power is one.
Example Question #3 : Finding Derivative Of A Function
What is the derivative of ?
To get , we can use the power rule.
Since the exponent of the is , as , we lower the exponent by one and then multiply the coefficient by that original exponent:
Anything to the power is .
Example Question #1 : Finding Derivative Of A Function
To solve this equation, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat as since anything to the zero power is one.
 "\frac{\mathrm{d} }{\mathrm{d} x}(6x^2+8)=(2*6x^{2-1})+(0*8x^{0-1})")
Notice that since anything times zero is zero.
Example Question #2 : Concept Of The Derivative
What is the derivative of ?
To solve this equation, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat as since anything to the zero power is one.
Notice that since anything times zero is zero.
That leaves us with .
Simplify.
As stated earlier, anything to the zero power is one, leaving us with:
Example Question #1 : Concept Of The Derivative
What is the derivative of ?
To solve this equation, we can use the power rule. To use the power rule, we lower the exponent on the variable and multiply by that exponent.
We're going to treat as since anything to the zero power is one.
 "\frac{\mathrm{d} }{\mathrm{d} x}(12x^2+13x+4)=(2*12x^{2-1})+(1*13x^{1-1})+(0*4x^{0-1})")
Notice that since anything times zero is zero.
Just like it was mentioned earlier, anything to the zero power is one.
Certified Tutor
Certified Tutor
All AP Calculus AB Resources
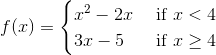
