All AP Calculus AB Resources
Example Questions
Example Question #2 : Calculus 3
Evaluate the following limit:
Does not exist.
First, let's multiply the numerator and denominator of the fraction in the limit by 
As 




The answer is 
Example Question #12 : Calculus 3
Let 


What is the value of 
Since 




We are asked to find 




The given information tells us that
The equation then becomes 
We can now solve for 

The answer is 
Example Question #11 : Fundamental Theorem Of Calculus
Using the fundamental theorem of calculus, find the integral of the function 


The fundamental theorem of calculus is, 
We can use the inverse power rule to solve the integral, which is 
Example Question #1 : How To Find Volume Of A Region
Consider the region bounded by the 



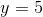
To find the volume, one would use the washer method:
For this problem: 
![V = \pi[\frac{20}{3}x^\frac{3}{2}} - \frac{x^{2}}{2}]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/117761/gif.latex)


Example Question #51 : Derivative As A Function
Find the area of the region enclosed by the parabola 

The two curves intersect in between 


To solve for the area between curves, 

For our problem:




Example Question #52 : Derivative As A Function
Find the area under the curve 

To find the area under the curve, we need to integrate. In this case, it is a definite integral.
Example Question #2 : Mean Value Theorem
Find the area bounded by
The easiest way to look at this is to plot the graphs. The shaded area is the actual area that we want to compute. We can first find area bounded by 



The area of the triangle above the curve 

Example Question #53 : Derivative As A Function
Example Question #4 : Mean Value Theorem
Consider the region bounded by the functions

between 

The area of this region is given by the following integral:

Taking the antiderivative gives





Thus, the area is given by:
Example Question #671 : Ap Calculus Ab
Let 
True or false: As a consequence of Rolle's Theorem, 

True
False
False
By Rolle's Theorem, if 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/969995/gif.latex)




All AP Calculus AB Resources

















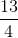





![=\left[ \frac{1^4}{4}+1^2+9(1)\right]-\left[\frac{0^4}{4}+0^2+9(0) \right ]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1002842/gif.latex)


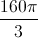

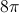

![V = \pi\int [R^{2}(x) - r^{2}(x)]dx.](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88472/gif.latex)
![V = \pi\int_{0}^{4} [5^{2} - (5-\sqrt{x})^{2} ]dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88473/gif.latex)
![V = \pi\int_{0}^{4} [25 - (25 - 10\sqrt{x}+ x)] dx](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/117760/gif.latex)

![V = \pi[\frac{20}{3}(4)\tfrac{3}{2} -\frac{4^{2}}{2} - (\frac{20}{3}(0)\tfrac{3}{2}-\frac{0^{2}}{2})]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/88476/gif.latex)
![V = \pi[(\frac{160}{3} - 8) - (0-0)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/117763/gif.latex)








































