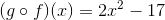We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Polynomial Functions

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

← Previous 1 2 3 4 5 6 7 Next →

Example Question #16 : Graphing Polynomial Functions

Define a function $f(x) = -3x^{2}+ 7x + 1$ .

Give the -coordinate of the -intercept of its graph.

Possible Answers:

$\frac{7}{6}$

Correct answer:

Explanation:

The -intercept of the graph of a function f(x) is the point at which it crosses the -axis; its -coordinate is 0, so its -coordinate is f(0) .

$f(x) = -3x^{2}+ 7x + 1$ ,

so, by setting x= 0 ,

$f(0) = -3 \cdot 0^{2}+ 7\cdot 0 + 1 = 0 + 0 + 1 = 1$ ,

making (0, 1) the -intercept.

Report an Error

Example Question #11 : Graphing Polynomial Functions

Try without a calculator.

The graph with the following equation is a parabola characterized by which of the following?

y= - 4x^2-12x+15

Possible Answers:

Concave upward

None of these

Concave downward

Concave to the right

Concave to the left

Correct answer:

Concave downward

Explanation:

The parabola of an equation of the form $y= ax^{2}+ bx + c$ is vertical, and faces upward or downward depending entirely on the sign of , the coefficient of $x^{2}$ . This coefficient, , is negative; the parabola is concave downward.

Report an Error

Example Question #18 : Graphing Polynomial Functions

P(x) is a polynomial function. P(0) = 4 , and P(x) has a zero on the interval (0,1 ) .

True or false: By the Intermediate Value Theorem, P(1)< 0

Possible Answers:

False

True

Correct answer:

False

Explanation:

As a polynomial function, the graph of P(x) is continuous. By the Intermediate Value Theorem, if P(a) < M < P(b) or P(b) < M < P(a) , then there must exist a value $c \in (a,b)$ such that P(c)= M .

Setting M = 0 , a = 0 and b= 1 , this becomes: If P(0) < 0 < P(1) or P(1) < 0 < P(0) , then there must exist a value $c \in (0,1)$ such that P(c)= 0 - that is, P(x) must have a zero on (0,1) .

However, the question is asking us to use the converse of this statement, which is not true in general. If P(x) has a zero on (0,1) , it does not necessarily follow that P(0) < 0 < P(1) or P(1) < 0 < P(0) - specifically, with P(0) = 4 > 0 , it does not necessarily follow that . A counterexample is the function shown below, which fits the conditions of the problem but does not have a negative value for P(1) :

Parabola

The answer is false.

Report an Error

Example Question #12 : Graphing Polynomial Functions

Try without a calculator.

The graph of a function with the given equation forms a parabola that is characterized by which of the following?

x=- 4y^2-12y+15

Possible Answers:

Concave downward

Concave to the left

None of these

Concave upward

Concave to the right

Correct answer:

Concave to the left

Explanation:

The graph of an equation of the form

x=ay^2+by+c

is a horizontal parabola. Whether it is concave to the left or to the right depends on the sign of . Since a = -4 , a negative number, the parabola is concave to the left.

Report an Error

Example Question #21 : Graphing Polynomial Functions

How many -intercepts does the graph of the following function have?

$f(x)= -4x^{2}+ 12x - 9$

Possible Answers:

One

Ten

Zero

Two

Five

Correct answer:

One

Explanation:

The graph of a quadratic function $f(x) = ax^{2}+ bx + c$ has an -intercept at any point (x,0 ) at which f(x) = 0 , so, first, set the quadratic expression equal to 0:

$-4x^{2}+ 12x - 9 = 0$

The number of -intercepts of the graph is equal to the number of real zeroes of the above equation, which can be determined by evaluating the discriminant of the equation, $b^{2} -4ac$ . Set a = -4, b = 12, c = -9 , and evaluate:

$b^{2} -4ac = 12^{2} - 4 (-4)(-9) = 144- 144 = 0$

The discriminant is equal to zero, so the quadratic equation has one real zero, and the graph of f(x) has exactly one -intercept.

Report an Error

Example Question #22 : Graphing Polynomial Functions

The vertex of the graph of the function

$f(x) = - x^{2} + 7x +11$

appears in __________.

Possible Answers:

Quadrant I

None of these

Quadrant IV

Quadrant III

Quadrant II

Correct answer:

Quadrant I

Explanation:

The graph of the quadratic function $f(x) = ax^{2} + bx+ c$ is a parabola with its vertex at the point with coordinates

$\left ( -\frac{b}{2a}, f \left (-\frac{b}{2a} \right ) \right )$ .

Set a = -1, b = 7 ; the -coordinate is

$-\frac{b}{2a} = - \frac{7}{2 \cdot (-1)} = -\frac{7}{-2} =\frac{7}{2} = 3\frac{1}{2}$ .

Evaluate $f \left ( \frac{7}{2} \right )$ by substitution:

$f(x) = - x^{2} + 7x +11$

$f \left ( \frac{7}{2} \right ) = - \left ( \frac{7}{2} \right ) ^{2} + 7 \left ( \frac{7}{2} \right ) +11$

$= - \frac{49}{4} + \frac{49}{2} +11$

$=23 \frac{1}{4}$

The vertex has a positive -coordinate and a positive -coordinate, putting it in the upper right quadrant, or Quadrant I.

Report an Error

Example Question #23 : Graphing Polynomial Functions

The vertex of the graph of the function

$f(x) = x^{2} + 7x - 9$

appears in __________.

Possible Answers:

Quadrant III

Quadrant IV

Quadrant I

None of these

Quadrant II

Correct answer:

Quadrant III

Explanation:

The graph of the quadratic function $f(x) = ax^{2} + bx+ c$ is a parabola with its vertex at the point with coordinates

$\left ( -\frac{b}{2a}, f \left (-\frac{b}{2a} \right ) \right )$ .

Set a = 1, b = 7 ; the -coordinate is $-\frac{b}{2a} = - \frac{7}{2 \cdot 1} = -\frac{7}{2} = -3\frac{1}{2}$ .

Evaluate $f \left ( -\frac{7}{2} \right )$ by substitution:

$f(x) = x^{2} + 7x - 9$

$f \left ( -\frac{7}{2} \right ) = \left ( -\frac{7}{2} \right )^{2} + 7 \left ( -\frac{7}{2} \right ) - 9$

$= \frac{49}{4} - \frac{49}{2} - 9$

$= - 21\frac{1}{4}$

The vertex has a negative -coordinate and a negative -coordinate, putting it in the lower left quadrant, or Quadrant III.

Report an Error

Example Question #1 : Transformations Of Polynomial Functions

$g(x)=4(2x-6)^{5}$

What transformations have been enacted upon g(x) when compared to its parent function, $f(x)=x^{5}$ ?