All Algebra II Resources
Example Questions
Example Question #31 : Polynomial Functions
A baseball is thrown off the roof of a building 220 feet high at an initial upward speed of 72 feet per second; the height of the baseball relative to the ground is modeled by the function
How long does it take for the baseball to reach its highest point (nearest tenth of a second)?
The highest point of the ball is the vertex of the ball's parabolic path, so to find the number of seconds 
The parabola of the graph of
has as its ordinate, or 

so, setting 

which rounds to 2.3 seconds. This is the time that it takes the ball to reach the highest point of its path.
Example Question #32 : Polynomial Functions
A baseball is thrown off the roof of a building 220 feet high at an initial upward speed of 72 feet per second; the height of the baseball relative to the ground is modeled by the function
How long does it take for the baseball to hit the ground (nearest tenth of a second)?
When the baseball hits the ground, its height is 0; therefore, we are looking for 

or
This equation can most easily be solved using the quadratic formula. If

then
Setting 
One possible answer is
We throw this out, since we cannot have "negative time".
The other is
This is positive, so we accept this answer. The ball hits the ground in about 6.6 seconds.
Example Question #579 : Functions And Graphs
Find the product:
Using the FOIL (first, outer, inner, last) method, you can expand the polynomial to get
first:
outer:
inner:
lasts:
From here, combine the like terms.
Example Question #581 : Functions And Graphs
What are the roots of 
In order to find the roots, we must factor the equation.
The factors of this equation are 

Setting those two equal to zero, we get 

Example Question #1 : Graphing Polynomial Functions
Where does the graph of 

To find where the graph crosses the horizontal axis, we need to set the function equal to 0, since the 

To find the possible rational zeroes of a polynomial, use the rational zeroes theorem:
Our constant is 10, and our leading coefficient is 1. So here are our possible roots:
Let's try all of them and see if they work! We're going to substitute each value in for 
Looks like that worked! We got 0 as our final answer after synthetic substitution. What's left in the bottom row helps us factor 
We keep doing this process until 
Thus, 


Example Question #22 : Graphing Functions
Where does 

5
7
-7
-3
3
7




Example Question #422 : Sat Subject Test In Math I
Which equation best represents the following graph?
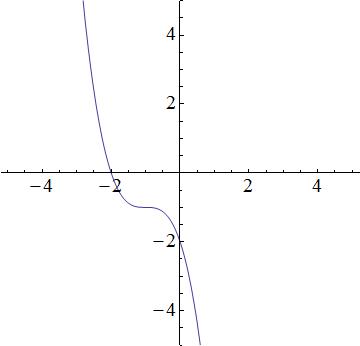
None of these
We have the following answer choices.
The first equation is a cubic function, which produces a function similar to the graph. The second equation is quadratic and thus, a parabola. The graph does not look like a prabola, so the 2nd equation will be incorrect. The third equation describes a line, but the graph is not linear; the third equation is incorrect. The fourth equation is incorrect because it is an exponential, and the graph is not an exponential. So that leaves the first equation as the best possible choice.
Example Question #1 : Understand Linear And Nonlinear Functions: Ccss.Math.Content.8.F.A.3
Which of the graphs best represents the following function?


None of these



The highest exponent of the variable term is two (
The graph below will be the answer, as it shows a parabolic curve.

Example Question #1 : Graphing Polynomial Functions
Turns on a polynomial graph.
What is the maximum number of turns the graph of the below polynomial function could have?
3 turns
4 turns
7 turns
8 turns
7 turns
When determining the maximum number of turns a polynomial function might have, one must remember:
Max Number of Turns for Polynomial Function = degree - 1
First, we must find the degree, in order to determine the degree we must put the polynomial in standard form, which means organize the exponents in decreasing order:
Now that f(x) is in standard form, the degree is the largest exponent, which is 8.
We now plug this into the above:
Max Number of Turns for Polynomial Function = degree - 1
Max Number of Turns for Polynomial Function = 8 - 1
which is 7.
The correct answer is 7.
Example Question #1 : Graphing Polynomial Functions
End Behavior
Determine the end behavior for 
In order to determine the end behavior of a polynomial function, it must first be rewritten in standard form. Standard form means that the function begins with the variable with the largest exponent and then ends with the constant or variable with the smallest exponent.
For f(x) in this case, it would be rewritten in this way:
When this is done, we can see that the function is an Even (degree, 4) Negative (leading coefficent, -3) which means that both sides of the graph go down infinitely.
In order to answer questions of this nature, one must remember the four ways that all polynomial graphs can look:
Even Positive:
Even Negative:
Odd Positive:
Odd Negative:
All Algebra II Resources







































































