All Algebra II Resources
Example Questions
Example Question #1 : Graphing Polynomial Functions
Which of the following is a graph for the following equation:
Cannot be determined

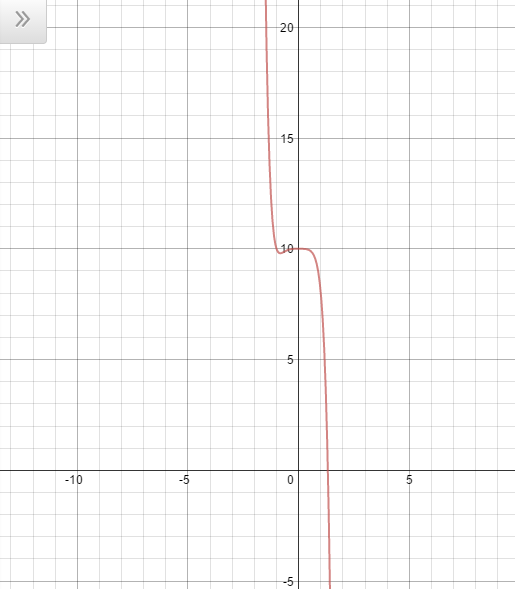



The way to figure out this problem is by understanding behavior of polynomials.
The sign that occurs before the 

Example Question #33 : Functions










None of the above



Starting with



Similarly 

Hence the correct answer is option 
Example Question #3 : Graphing Polynomial Functions
When we look at the function we see that the highest power of the function is a 3 which means it is an "odd degree" function. This means that the right and left side of the function will approach opposite directions. *Remember O for Odd and O for opposite.
In this case we also have a negative sign associated with the highest power portion of the function - this means that the function is flipped.
Both of these combine to make this an "odd negative" function.
Odd negative functions always have the right side of the function approaching down and the left side approaching up.
We represent this mathematically by saying that as x approaches negative infinity (left side), the function will approach positive infinity:
...and as x approaches positive infinity (right side) the function will approach negative infinity:
Example Question #4 : Graphing Polynomial Functions
Then set each factor equal to zero, if any of the ( ) equal zero, then the whole thing will equal zero because of the zero product rule.
Example Question #41 : Polynomial Functions



True or false: By the Intermediate Value Theorem, 

False
True
False
As a polynomial function, the graph of 




Set 





Both are polynomial graphs fitting the given conditions, but the only the equation graphed at right has a zero on 
Example Question #42 : Polynomial Functions
How many 
have?
Two
Zero
One
Two
The graph of a quadratic function 



Since the question simply asks for the number of 
is

Set 
The discriminant is positive, so the 

Example Question #43 : Polynomial Functions
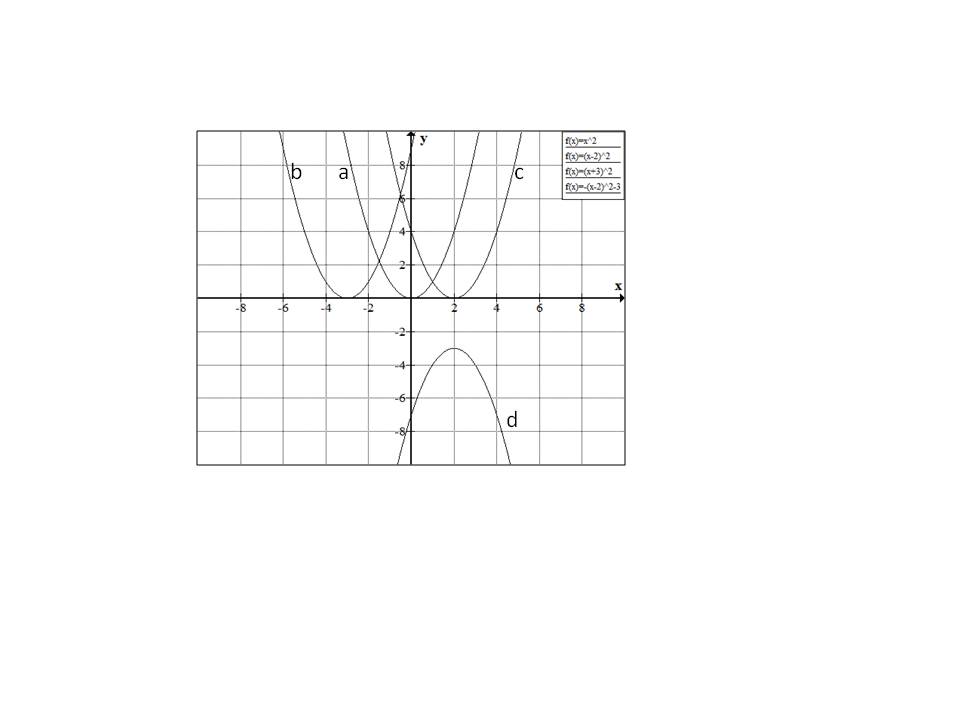
The vertex of the graph of the function
appears ________
in Quadrant I.
in Quadrant III.
on an axis.
in Quadrant II.
in Quadrant IV.
on an axis.
The graph of the quadratic function 

Set 

Evaluate 
The vertex has 0 as its 
Example Question #44 : Polynomial Functions



True, false, or undetermined: 

Undetermined
True
False
True
As a polynomial function, the graph of 




Setting 
if 








Example Question #45 : Polynomial Functions





True or false: By the Intermediate Value Theorem, 
True
False
True
As a polynomial function, the graph of 




Setting 







However, the conclusion of this statement is false: 






Example Question #142 : Functions And Graphs

Which of the following is an equation for the above parabola?
The zeros of the parabola are at 


each of their signs is reversed to end up with the correct sign in the answer. The coefficient can be found by plugging in any easily-identifiable, non-zero point to the above formula. For example, we can plug in 

All Algebra II Resources