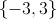Whenever you see the difference of two cubes - as you do here with  and , which is , you can apply the formula for Difference of Cubes to factor that term:

Here that means you can follow the template with  and  to get:

Whenever you see the sum of two cubes, as you do here since  and , you can factor that sum using the formula:

Here that allows you to replace  with  and  with  to get:

This problem has you go backward from a notable rule, the Sum of Cubes rule. You should recognize the Sum of Cubes as .  Here you should see the familiar symptoms of that rule: in the rightmost set of parentheses, you have two squared terms,  and , and you have their square roots ( and ) in the leftmost set. Once you've determined that you're dealing with the Sum of Cubes structure, the conversion should be relatively quick without having to distribute the multiplication manually.

This problem employs the Sum of Cubes rule, which states that:

Here you should see that the given expression, , can be written as a sum of two cubes: . This allows you to invoke the formula, resulting in:

This problem calls on your knowledge of the Difference of Cubes rule, which states that:

Here you're given two parentheticals in this exact form, allowing you to invoke the rule to solve without manually expanding the parentheses through multiplication. Your  and  terms are  and , so you can simply express the answer as .

By substituting  - and, subsequently,  this can be rewritten as a quadratic equation, and solved as such:

We are looking to factor the quadratic expression as , replacing the two question marks with integers with product  and sum 5; these integers are .

Substitute back:

The first factor cannot be factored further. The second factor, however, can itself be factored as the difference of squares:

Set each factor to zero and solve:

Since no real number squared is equal to a negative number, no real solution presents itself here. 

The solution set is .

Rewriting the equation as , we can see there are four terms we are working with, so factor by grouping is an appropriate method. Between the first two terms, the Greatest Common Factor (GCF) is  and between the third and fourth terms, the GCF is 4. Thus, we obtain .   Setting each factor equal to zero, and solving for , we obtain  from the first factor and  from the second factor. Since the square of any real number cannot be negative, we will disregard the second solution and only accept . 

The first step is to determine if all of the terms have a greatest common factor (GCF). Since a GCF does not exist, we can move onto the next step.

Create smaller groups within the expression. This is typically done by grouping the first two terms and the last two terms.

Factor out the GCF from each group:

At this point, you can see that the terms inside the parentheses are identical, which means you are on the right track!

Since there is a GCF of (5x+1), we can rewrite the expression like this:

And that is your answer! You can always check your factoring by FOILing your answer and checking it against the original expression.

This can be most easily solved by setting  and, subsequently, . This changes the degree-4 polynomial in  to one that is quadratic in , which can be solved as follows:

The quadratic factors do not fit any factoring pattern and are prime, so this is as far as the polynomial can be factored.

To find , we must start inwards and work our way outwards, i.e. starting with :

We can now use this value to find  as follows:

Our final answer is therefore