Algebra II : Algebra II
Study concepts, example questions & explanations for Algebra II
All Algebra II Resources
Example Questions
Example Question #1 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of
Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
Odd symmetry
Even symmetry
No symmetry
Even symmetry
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. We can see that what is on the left side of the line x=0 is an exact match of what is on the right side of the line x=0. Therefore, this graph has even symmetry. Algebraically, a function has even symmetry if f(x)=f(-x). You can plug in several test values of x to see this for yourself.
Example Question #1 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of
Select the choice that correctly indicates this graph's end behavior.
As
As
As
As
As
As
As
As
As
As
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting bigger and bigger (more and more positive.) Therefore, as x approaches negative infinity, y approaches infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As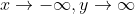 
Example Question #3 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of
Select the choice that correctly indicates this graph's end behavior.
As
As
As
As
As
As
As
As
As
As
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting bigger and bigger (more and more positive.) Therefore, as x approaches negative infinity, y approaches infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, y gets more and more negative. Therefore as x approaches infinity, y approaches negative infinity. Mathematically, this is written like:
As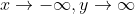 
Example Question #4 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of
Select the choice that correctly indicates this graph's end behavior.
As
As
As
As
As
As
As
As
As
As
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As 
Example Question #1 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of
Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
This graph has odd symmetry.
This graph has even symmetry.
This graph does not have any symmetry.
This graph has odd symmetry.
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. Quadrant I (x and y both positive) has a piece of the graph, while Quadrant II (x negative, y positive) has no part of the graph. Because these are not matching, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does have this quality, so it has odd symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see this for yourself.
Example Question #6 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of
Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
This graph has even symmetry.
This graph has odd symmetry.
This graph has no symmetry.
This graph has no symmetry.
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. Quadrant I (x and y both positive) has a piece of the graph as does Quadrant II (x negative, y positive); however, these pieces are not mirror images of one another. Therefore, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. In the original graph, the graph flattens above the origin, but if we flip this upside down, it flattens below the origin. While it has odd symmetry around the point (0, 5), it does not have symmetry around the origin, and therefore the function is not odd. Therefore, this graph does not have symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see that neither of these are satisfied.
Example Question #1 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of
Select the choice that correctly indicates this graph's end behavior.
As
As
As
As
As
As
As
As
As
As
When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Then start again at the origin, this time moving right. You can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:
As
Example Question #1 : Extrema, End Behavior, And Graph Symmetry
Below is the graph of
Select the choice that correctly indicates whether this graph has even symmetry, odd symmetry, or neither.
This graph has odd symmetry.
This graph has no symmetry.
This graph has even symmetry.
This graph has odd symmetry.
The question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. Quadrant I (x and y both positive) has no piece of this graph, while Quadrant II (x negative, y positive) has a part of the graph. Because these are not matching, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does have this quality, so it has odd symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x). You can plug in several test values of x to see this for yourself.
Example Question #1 : System Of Equations
This graph shows a solution at its intersection, the point (1,-1). This solution could be the solution for which of the following systems of equations?
Based on the graph, you can see that the purple line has the equation 
Example Question #2 : System Of Equations
10 workouts
8 workouts
2 workouts
5 workouts
8 workouts
A system of equations that models this, where a is the number of workouts Alf has completed and t is the number of workouts Tanner has completed is:
Next, graph each of these equations:
Then, identify where the two lines meet each other. This is at (2,8). Therefore, after they each complete 8 workouts (in 2 weeks time) they will have completed the same number of workouts.
Certified Tutor
Certified Tutor
All Algebra II Resources
