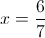Using the difference of cubes formula:

Find x and y:

Plug into the formula:

Which Gives:

And cannot be factored more so the above is your final answer.

First, we can factor a  from both terms:

Now we can make a clever substitution.  If we make  the function now looks like:

This makes it much easier to see how we can factor (difference of squares):

The last thing we need to do is substitute  back in for , but we first need to solve for  by taking the square root of each side of our substitution:

Substituting back in gives us a result of:

Use the difference of squares to factor out the numerator.

The term  is prime, but  can still be factored by another difference of squares.

Replace the fraction.

Simplify the top and bottom.

The answer is:  

The degree is the highest exponent value of the variables in the polynomial.

Here, the highest exponent is x⁵, so the degree is 5.

By the Rational Zeroes Theorem, any rational solution must be a factor of the constant, 6, divided by the factor of the leading coefficient, 14. 

Four of the answer choices have this characteristic:

is in lowest terms, and 3 is not a factor of 14. It is therefore the correct answer.

This can be written as:

Multiply the terms together:

Multiply the first two terms:

FOIL:

Combine like terms:

from the zeroes given and the Fundamental Theorem of Algebra we know:

use FOIL method to obtain:

Distribute:

Simplify:

Find a polynomial function  of the lowest order possible such that two of the roots of the function are: 

Recall that by roots of a polynomial we are referring to values of  such that . 

Because one of the roots given is a complex number, we know there must be a second root that is the complex conjugate of the given root. This is . 

Because  is a root, the unknown function  must have a factor 

The other roots are complex numbers, so there must be a quadratic factor.

To find the quadratic factor start with the  value for one of the complex roots: 

Isolate the imaginary term  onto one side and square, 

Expand the left side, and note on the right side the  factor reduces as follows: 

So now we have, 

The quadratic factor for  is therefore  . Combining this with the  factor give a factored expression for the desired function: 

Now we carry out the multiplication to write the final form of , 

When you're writing a quadratic having been given its zeros, the best place to start is by setting aside the coefficient and first putting together a simple, factored quadratic that would satisfy those zeros.  Here with zeros at 7 and -3, that would be:

If you then expand that quadratic, you have:

Of course, that's just one possible quadratic that satisfies those zeros, and your job is to find THE quadratic that satisfies those zeroes AND passes through (0, -63).  And clearly here if you plug in  to the quadratic you would not get . So your next step is to determine the coefficient. You can do that by setting the value of the coefficient as :

And then plugging in  since you know that when .

So 

Meaning that .  You can then multiply the original quadratic by 3 to get:

A quadratic function takes the form  where x is a variable and a, b, and c are coefficients. Equations of this nature can be factored, and then each factor can be set equal to zero and then solved to find the roots of the equation. This problem asks you to take that idea, but work through it in reverse. To solve it, begin with:

 and 

Get everyone on one side of the equation:

 and 

These are the factors of the equation. Put them together, and then multiply them to get:

Therefore, the solution to this question is