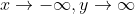We can use process of elimination to find the correct answer.

It can't be Imaginary because we're not dividing by a negative number.

It can't be Complex because the number's aren't a mix of real and imaginary numbers.

It can't be Irrational because they aren't fractions.

It can't be Natural because there are negative numbers.

It must be Integers then!  All the numbers are whole numbers that fit on the number line.

Any even power of the imaginary unit  is a real number. For example, 

 from the definition of  as the principal square root of .

Also, from the Power of a Power Property,

 or A intersect B means what A and B have in common.

In this case both A and B have the numbers 1, 9, and 11.

To raise  to the power of any positive integer, divide the integer by 4 and note the remainder. The correct power is given according to the table below.

Every element in the set  is equal to  raised to an odd-numbered power, so when each exponent is divided by 4, the remainder will be either 1 or 3. Therefore, each element is equal to either  or . Consequently, the set includes only imaginary numbers.

Start by making a list of the multiples of 4 that are smaller than the square of 7. When 7 is squared, it equals 49; thus, we can compose the following list:

Next, make a list of all the multiples of 6 that are greater than 0. Since we are looking for shared multiples, stop after 48 because numbers greater than 48 will not be included in set A. The biggest multiple of 4 smaller that is less than 49 is 48; therefore, do not calculate multiples of 6 greater than 48.

Finally, count the number of multiples found in both sets. Both sets include the following numbers:

The correct answer is 4 numbers.

The easiest approach to this problem is to pick a value for X, and plug it in.

If we use , then then expression

a) .

b)

c)

The order from least to greatest is C,B,A

, remembering that, then the most negative number is first, the least negative is last. 

Therefore,

.

Thus when we put them in order we get,

Integers are values you would find on a number line.

They are whole numbers that exist in positive and negative values. What divides them is the number .

So integers are essentially positive, negative whole numbers and .

The answer will lie in the range between negative one and a half.  Convert all the values given to integer or fractional form.

 is undefined.

Of all the possible answers,  will fall between the given range.

The answer is:  

To get started on this problem, it helps to use a graphing calculator or other graphing tool to visualize the function. The graph of  is below:

When identifying end behavior, you want to ask yourself "As x gets infinitely big/small, what happens to y?" If you start at x=0, then move left to where x=-1, you can see that the values of y are getting smaller and smaller (more and more negative.) Therefore, as x approaches negative infinity, y also approaches negative infinity. Next, look at x=2, then x=3, and so on, and you can see that as x gets bigger and bigger, so too does y. Therefore as x approaches infinity, y also approaches infinity. Mathematically, this is written like:

As  and as .

Next, the question asks to identify any local minima and maxima. It helps to think of these as "peaks" and "valleys." Looking at the graph, it appears that these exist at the points (0, 1) and (2, -3). We can check this algebraically by plugging in these x values and seeing that the associated y values come out of the function. 

This confirms that the point (0, 1) is a local maxima (peak) and the point (2, -3) is a local minima (valley).

Finally, the question asks us to determine whether the graph has even, odd, or no symmetry. In order for a graph to have even symmetry, it must produce the same image when reflected over the y-axis. The right side of this graph has a local minima, while the left side does not, therefore, this graph is not even. In order to have odd symmetry, the graph must have symmetry over the line y=x. An easy way to spot this is to see if the graph looks the same right side up as it does upside down. This does not, therefore, the graph has no symmetry. Algebraically, a function has even symmetry if f(x)=f(-x), and a function has odd symmetry if -f(x)=f(-x).