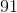We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

Create An Account

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #10 : Graphing Hyperbolic Inequalities

Which graph represents the inequality $[(y-1)^2]/1 - [(x+2)^2]/9 \geq 1$ ?

Possible Answers:

Screen shot 2020 08 26 at 8.33.13 am

Screen shot 2020 08 26 at 8.35.55 am

Screen shot 2020 08 26 at 8.34.53 am

Screen shot 2020 08 26 at 8.36.21 am

Correct answer:

Screen shot 2020 08 26 at 8.33.13 am

Explanation:

The equation for a horizontal hyperbola is [(x-h)^2]/(a^2) - [(y-v)^2]/(b^2) = 1 . The equation for a vertical hyperbola is [(y-v)^2]/(b^2) - [(x-h)^2]/(a^2) = 1 . In both, (h, v) is the center of the hyperbola. Hyperbolic inequalities use an inequality sign rather than an equals sign, but otherwise have the same form as hyperbolic equations. The x and y in the inequality are followed by the constants 2 and -1 respectively, so the graph must be centered on (-2, 1). The y-term appears first, so the graph must show a vertical hyperbola. The inequality sign is $\geq$ rather than , so the lines must be solid rather than dashed. The left side is greater than rather than less than the constant, so the center must not be shaded.

Report an Error

Example Question #1 : How To Find The Degree Of A Polynomial

Give the degree of the polynomial.

$6x^{5}+5x^{4}-3x^{2}+x^{7}$

Possible Answers:

Correct answer:

Explanation:

$6x^{5}+5x^{4}-3x^{2}+x^{7}$

The degree of an individual term of a polynomial is the exponent of its variable; the exponents of the terms of this polynomial are, in order, 5, 4, 2, and 7.

The degree of the polynomial is the highest degree of any of the terms; in this case, it is 7.

Report an Error

Example Question #1 : How To Find The Degree Of A Polynomial

What is the degree of the polynomial?

$ab^{2}+a^{2}b^{3}-a^{3}b^{1}$

Possible Answers:

Correct answer:

Explanation:

$ab^{2}+a^{2}b^{3}-a^{3}b^{1}$

To find the degree of the polynomial, you first have to identify each term [term is for example $ab^{2}$ ], so to find the degree of each term you add the exponents.

EX: $ab^{2}$ $= a^{1}b^{2} = 1+2= 3$ - Degree of 3

Highest degree is $5\rightarrow$ $a^{2}b^{3}= 2+3= 5$

Report an Error

Example Question #2 : How To Find The Degree Of A Polynomial

What is the degree of the polynomial?

12x^2y^3+6xy^4z-2xz+1

Possible Answers:

Correct answer:

Explanation:

To find the degree of the polynomial, add up the exponents of each term and select the highest sum.

12x²y³: 2 + 3 = 5

6xy⁴z: 1 + 4 + 1 = 6

2xz: 1 + 1 = 2

The degree is therefore 6.

Report an Error

Example Question #1 : Polynomial Functions

Let $\small f(x)=x^2-10$ , $\small g(x)=x^3$ , and $\small h(x)=2x$ . What is $\small f(h(g(x)))$ ?

Possible Answers:

$\small \small 2x^6-10$

$\small 4x^6-10$

$\small 6x^2-60$

$\small 64x^6-10$

$\small 8x^6-240x^4+960x^2-8000$

Correct answer:

$\small 4x^6-10$

Explanation:

When solving functions within functions, we begin with the innermost function and work our way outwards. Therefore:

$\small h(g(x))=2(x^3)=2x^3$

and

$\small f(h(g(x)))=(2x^3)^2-10=4x^6-10$

Report an Error

Example Question #2 : Polynomial Functions

Let $\small f(x)=\sqrt[3]{x^2}$ , $\small g(x)=x^3$ , and $\small h(x)=\sqrt[4]{x}$ . What is $\small f(g(h(x)))$ ?

Possible Answers:

$\small \sqrt[3]{x^2}$

$\small \sqrt{x}$

$\small \sqrt[4]{x^3}$

$\small \sqrt[3]{x}$

$\small \sqrt[4]{x}$

Correct answer:

$\small \sqrt{x}$

Explanation:

This problem relies on our knowledge of a radical expression $\small \sqrt[b]{x^a}$ equal to $\small x^\frac{a}{b}$ . The functions are subbed into one another in order from most inner to most outer function.

$\small g(h(x))=(\sqrt[4]{x})^3=x^\frac{3}{4}$

and

$\small f(g(h(x)))=\sqrt[3]{(x^\frac{3}{4})^2}=\sqrt[3]{x^\frac{6}{4}}=x^\frac{6}{12}=x^\frac{1}{2}=\sqrt{x}$

Report an Error

Example Question #2 : Polynomial Functions

Evaluate $\small f(g(9))$ if $\small f(x) = x^2 + 10$ and $\small g(x) = \sqrt{x^2 -5x+13}$

Possible Answers:

7839

$\textup{Undefined}$

Correct answer:

Explanation:

In problems with functions within one another, we must first solve the innermost function and then proceed outwards. Therefore, the first step is solving $\small g(9)$ :

$\small g(9) =\small \sqrt{(9)^2 - 5(9)+13}=\sqrt{81-45+13}=\sqrt{49}=\pm7$

Now, we must find the values of $\small f(\pm 7)$ :

$\small f(\pm 7)= (\pm 7)^2 +10=49+10=59$

Because our x term is squared in this function, both values end up being the same. Therefore, 59 is our final answer.

Report an Error

Example Question #1 : Polynomial Functions

Evaluate $\small f(g(-9))$ if $\small \small f(x)=\sqrt{x^2-4}$ and $\small g(x)=-\frac{1}{3}x - 2$

Possible Answers:

$\textup{Undefined}$

$\small -\frac{38}{3}$

Correct answer:

$\textup{Undefined}$

Explanation:

Beginning with the innermost function, we must first solve for $\small \small g(-9)$ :

$\small g(9)=-\frac{1}{3}(-9)-2=3-2=1$

We then take this value and plug it into $\small f(x)$ :

$\small f(1)=\sqrt{(1)^2-4}=\sqrt{-3}$

This has no value in the real number plane, and the answer is therefore undefined.

Report an Error

Example Question #1 : Polynomial Functions

g(x)=f(-x) and $f(x)=-3x^{2}-7x+4$ .

Determine g(x) .

Possible Answers:

$-3x^{2}-7x+4$

$3x^{3}+7x^{2}-4x$

$3x^{2}+7x+4$

$-3x^{2}+7x-4$

$-3x^{2}+7x+4$

Correct answer:

$-3x^{2}+7x+4$

Explanation:

Substituting -x into f(x). This has no effect on the 1st and 3rd terms. This changes the sign of the middle term.

Report an Error

Example Question #1071 : Algebra Ii

Which of the following depicts a polynomial in standard form?

Possible Answers:

$\small 2+6x+x^2+x^4$

None of the other answers are correct.

$\small 6+5x+3x^4+2x^2+x^3$

$\small x^4+x^2+6x-2$

$\small x^3+2x^2+3x^4+5x+6$

Correct answer:

$\small x^4+x^2+6x-2$

Explanation:

A polynomial in standard form is written in descending order of the power. The highest power should be first, and the lowest power should be last.

$\small \small x^4+x^2+6x-2$

The answer has the powers decreasing from four, to two, to one, to zero.

Report an Error

View Algebra 2 Tutors

Abe
Certified Tutor

CUNY Brooklyn College, Bachelor of Science, Accounting and Business Management. CUNY Graduate School and University Center, M...

View Algebra 2 Tutors

Oliver
Certified Tutor

Bard College, Bachelor of Science, Mathematics.

View Algebra 2 Tutors

Jacob
Certified Tutor

Ohio State University-Main Campus, Bachelor of Science, Political Science and Government.

All Algebra II Resources

10 Diagnostic Tests 630 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

SSAT Tutors in Atlanta, SAT Tutors in Washington DC, English Tutors in Miami, ISEE Tutors in Chicago, Algebra Tutors in San Diego, MCAT Tutors in Seattle, LSAT Tutors in Houston, SSAT Tutors in Dallas Fort Worth, Reading Tutors in Atlanta, Reading Tutors in Chicago

Popular Courses & Classes

Spanish Courses & Classes in Seattle, SAT Courses & Classes in Denver, GMAT Courses & Classes in San Diego, GRE Courses & Classes in Seattle, GMAT Courses & Classes in Atlanta, LSAT Courses & Classes in Washington DC, ACT Courses & Classes in Chicago, ISEE Courses & Classes in Denver, MCAT Courses & Classes in Boston, GMAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

GRE Test Prep in Boston, GRE Test Prep in Houston, SAT Test Prep in Miami, SAT Test Prep in Los Angeles, ISEE Test Prep in Washington DC, SAT Test Prep in Atlanta, GMAT Test Prep in Dallas Fort Worth, GMAT Test Prep in San Diego, MCAT Test Prep in Miami, SAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

Algebra II : Algebra II

Study concepts, example questions & explanations for Algebra II

All Algebra II Resources

Example Questions

Example Question #10 : Graphing Hyperbolic Inequalities

Example Question #1 : How To Find The Degree Of A Polynomial

Example Question #1 : How To Find The Degree Of A Polynomial

Example Question #2 : How To Find The Degree Of A Polynomial

Example Question #1 : Polynomial Functions

Example Question #2 : Polynomial Functions

Example Question #2 : Polynomial Functions

Example Question #1 : Polynomial Functions

Example Question #1 : Polynomial Functions

Example Question #1071 : Algebra Ii

All Algebra II Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: