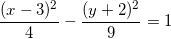All Algebra II Resources
Example Questions
Example Question #103 : Quadratic Functions
What are the coordinates of the center of the hyperbolic inequality ![\frac{[(y+2)^{2}]}{9}-\frac{[(x-1)^{2}]}{4}\geq 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1174381/gif.latex)
The equation for a horizontal hyperbola is ![\frac{[(x-h)^{2}]}{(a^{2})}-\frac{[(y-v)^{2}]}{(b^{2})}=1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1174382/gif.latex)
![\frac{[(y-v)^{2}]}{(b^{2})}-\frac{[(x-h)^{2}]}{(a^{2})}=1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1174383/gif.latex)
The graph of the hyperbolic inequality ![\frac{[(y+2)^{2}]}{9}-\frac{[(x-1)^{2}]}{4}\geq 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1174384/gif.latex)

With vertices of (1, 1) and (1, -5), you can see that the midpoint between them is (1, -2).
Example Question #104 : Quadratic Functions
What are the coordinates of the center of the hyperbolic inequality ![\frac{[(x+3)^{2}]}{9}-\frac{(y^{2})}{4}< 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1174377/gif.latex)
The equation for a horizontal hyperbola is ![\frac{[(x-h)^{2}]}{(a^{2})}-\frac{[(y-v)^{2}]}{(b^{2})}=1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1174378/gif.latex)
![\frac{[(y-v)^{2}]}{(b^{2})}-\frac{[(x-h)^{2}]}{(a^{2})}=1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1174379/gif.latex)
The graph of the hyperbolic inequality ![\frac{[(x-h)^{2}]}{(a^{2})}-\frac{[(y-v)^{2}]}{(b^{2})}=1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1174380/gif.latex)

As you can see, the midpoint between the two vertices of (-6, 0) and (0, 0) is (-3, 0).
Example Question #105 : Quadratic Functions
Which equation does this graph represent?

The equation for a horizontal hyperbola is ![[(x-h)^2]/(a^2) - [(y-v)^2]/(b^2) = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1171995/gif.latex)
![[(y-v)^2]/(b^2) - [(x-h)^2]/(a^2) = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1171996/gif.latex)
Example Question #12 : Hyperbolic Functions
In which direction does the graph of the hyperbola ![[(x-3)^2]/100 - [(y-4)^2]/144 = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172136/gif.latex)
vertical
horizontal
horizontal
The equation for a horizontal hyperbola is ![[(x-h)^2]/(a^2) - [(y-v)^2]/(b^2) = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172031/gif.latex)
![[(y-v)^2]/(b^2) - [(x-h)^2]/(a^2) = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1172032/gif.latex)
Example Question #511 : Functions And Graphs
In which direction does the graph of the above hyperbola open?
vertical
horizontal
horizontal
To determine which direction a hyperbola opens, first get the equation into standard form for a conic section:
This equation gives us a hyperbola when the coefficient in front of either the x-squared or the y-squared term (but not both!) is negative. In this problem, the coefficient in front of the x-squared term is positive, but the coefficient of the y-squared term is negative. Here are the rules for hyperbola directions:
- If the coefficient of the x-squared term is positive but the coefficient of the y-squared term is negative, this is a hyperbola that opens horizontally.
- If the coefficient of the x-squared term is negative but the coefficient of the y-squared term is positive, this is a hyperbola that opens vertically.
Thus, we have a graph of a horizontal hyperbola.
Example Question #2 : Graphing Hyperbolic Functions
What are the vertices of this hyperbola?


The first thing we need to find for this hyperbola is the center. This is simply the point where 





The denominator is 




Example Question #2 : Graphing Hyperbolic Functions
Write the expression for this hyperbola in standard form:
The standard form of a hyperbola is
or the similar form with a positive 



the coefficient of 

and similarly with 
and so our starting expression can be written as
Dividing by 
Example Question #1 : Graphing Hyperbolic Functions
Find the vertices of the following hyperbolic function:
We start by noticing that our hyperbola is given in the following form:
In order to determine the vertices of the hyperbola, we must first locate its center. Using the standard form given above, we know the center of the hyperbola occurs at the point (h,k), so for the equation given in the problem the center is at (2,-3). Now that we know the location of the hyperbola's center, our next step is to determine how far the vertices are from the center of the hyperbola. Looking at our equation, we can see it is in the form where the x term occurs first, which means the hyperbola opens left and right as opposed to up and down (which would be the case if the y term occurred first. Given this information, we know the vertices of the hyperbola are going to be a distance 



Example Question #1 : Graphing Parabolic Inequalities
Give the solution set of the inequality:
The inequality has no solution
Rewrite in standard form and factor:
The zeroes of the polynomial are therefore 




Test 

False; 

Test
True; 

Test 
False; 
Since the inequality symbol is 

Example Question #1 : Graphing Parabolic Inequalities
Give the set of solutions for this inequality:
This inequality has no solution.
The first step of questions like this is to get the quadratic in its standard form. So we move the 
This quadratic can easily be factored as
and look at each of the factors individually. Recall that a negative number times a negative is a positive number. Therefore the boundaries of our solution interval is going to be when both of these factors are negative. 





Our other boundary will be the other point when the product of the factors becomes positive. Remember that 


Certified Tutor
Certified Tutor
All Algebra II Resources









![[(x+2)^2]/1 + [(y+1)^2]/4 = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1171980/gif.latex)
![[(y+1)^2]/4 - [(x+2)^2]/1 = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1171981/gif.latex)
![[(y+1)^2]/4 + [(x+2)^2]/1 = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1171982/gif.latex)
![[(x+2)^2]/1 - [(y+1)^2]/4 = 1](http://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/1171979/gif.latex)