All Algebra II Resources
Example Questions
Example Question #1 : Graphing Polynomial Functions
End Behavior
Determine the end behavior for 
In order to determine the end behavior of a polynomial function, it must first be rewritten in standard form. Standard form means that the function begins with the variable with the largest exponent and then ends with the constant or variable with the smallest exponent.
For f(x) in this case, it would be rewritten in this way:
When this is done, we can see that the function is an Even (degree, 4) Negative (leading coefficent, -3) which means that both sides of the graph go down infinitely.
In order to answer questions of this nature, one must remember the four ways that all polynomial graphs can look:
Even Positive:
Even Negative:
Odd Positive:
Odd Negative:
Example Question #1 : Graphing Polynomial Functions
Which of the following is a graph for the following equation:
Cannot be determined

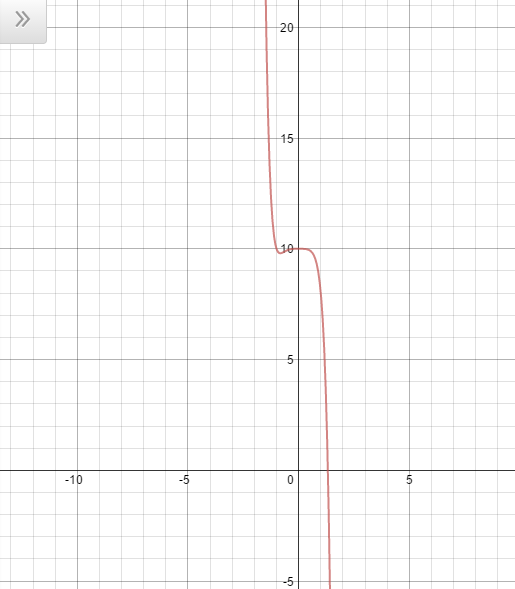



The way to figure out this problem is by understanding behavior of polynomials.
The sign that occurs before the 

Example Question #35 : Functions








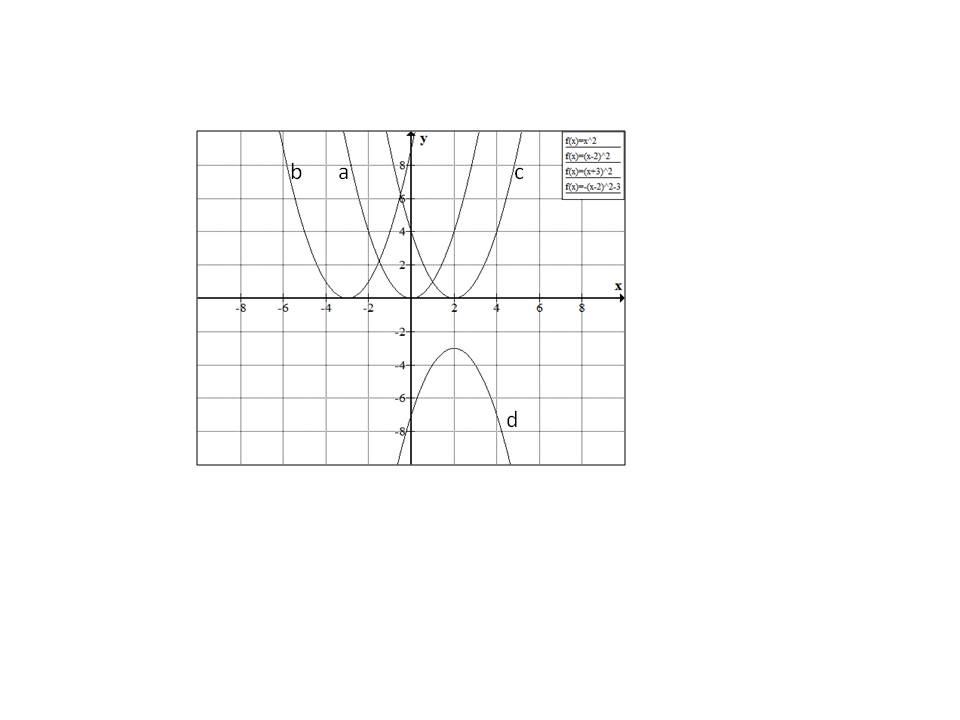




None of the above

Starting with



Similarly 

Hence the correct answer is option 
Example Question #3 : Graphing Polynomial Functions
When we look at the function we see that the highest power of the function is a 3 which means it is an "odd degree" function. This means that the right and left side of the function will approach opposite directions. *Remember O for Odd and O for opposite.
In this case we also have a negative sign associated with the highest power portion of the function - this means that the function is flipped.
Both of these combine to make this an "odd negative" function.
Odd negative functions always have the right side of the function approaching down and the left side approaching up.
We represent this mathematically by saying that as x approaches negative infinity (left side), the function will approach positive infinity:
...and as x approaches positive infinity (right side) the function will approach negative infinity:
Example Question #4 : Graphing Polynomial Functions
Then set each factor equal to zero, if any of the ( ) equal zero, then the whole thing will equal zero because of the zero product rule.
Example Question #41 : Polynomial Functions



True or false: By the Intermediate Value Theorem, 

False
True
False
As a polynomial function, the graph of 




Set 





Both are polynomial graphs fitting the given conditions, but the only the equation graphed at right has a zero on 
Example Question #42 : Polynomial Functions
How many 
have?
Two
Zero
One
Two
The graph of a quadratic function 



Since the question simply asks for the number of 
is

Set 
The discriminant is positive, so the 

Example Question #43 : Polynomial Functions
The vertex of the graph of the function
appears ________
in Quadrant I.
in Quadrant III.
on an axis.
in Quadrant II.
in Quadrant IV.
on an axis.
The graph of the quadratic function 

Set 

Evaluate 
The vertex has 0 as its 
Example Question #44 : Polynomial Functions



True, false, or undetermined: 

Undetermined
True
False
True
As a polynomial function, the graph of 




Setting 
if 








Example Question #45 : Polynomial Functions





True or false: By the Intermediate Value Theorem, 
True
False
True
As a polynomial function, the graph of 




Setting 







However, the conclusion of this statement is false: 






Certified Tutor
All Algebra II Resources