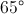Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #12 : Acute / Obtuse Triangles

Triangle_a

Figure NOT drawn to scale.

If $x = 72^{\circ }$ and $y = 43^{\circ }$ , evaluate .

Possible Answers:

$125^{\circ }$

$65^{\circ}$

$115^{\circ }$

$137^{\circ}$

$108^{\circ}$

Correct answer:

$115^{\circ }$

Explanation:

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

$w = x + y = 72 + 43 = 115 ^{\circ }$

Report an Error

Example Question #223 : Geometry

If the vertex angle of an isoceles triangle is $64^{\circ}$ , what is the value of one of its base angles?

Possible Answers:

$36^{\circ}$

$64^{\circ}$

$116^{\circ}$

$58^{\circ}$

$26^{\circ}$

Correct answer:

$58^{\circ}$

Explanation:

In an isosceles triangle, the base angles are the same. Also, the three angles of a triangle add up to $180^{\circ}$ .

So, subtract the vertex angle from $180^{\circ}$ . You get $116^{\circ}$ .

Because there are two base angles you divide $116^{\circ}$ by , and you get $58^{\circ}$ .

Report an Error

Example Question #13 : Acute / Obtuse Triangles

Triangle

Note: Figure NOT drawn to scale.

Refer to the above diagram.

$45^{\circ } \leq m \angle 1 \leq 50^{\circ }$

$60^{\circ } \leq m \angle 2 \leq 70 ^{\circ }$

Which of the following could be a measure of $\angle 3$ ?

Possible Answers:

$100^{\circ }$

$125^{\circ }$

$130^{\circ }$

All of the other choices give a possible measure of $\angle 3$ .

$110^{\circ }$

Correct answer:

$110^{\circ }$

Explanation:

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

$\angle 3 = \angle 1 + \angle 2$ .

We also have the following constraints:

$45^{\circ } \leq m \angle 1 \leq 50^{\circ }$

$60^{\circ } \leq m \angle 2 \leq 70 ^{\circ }$

Then, by the addition property of inequalities,

$45^{\circ } + 60 ^{\circ }\leq m \angle 1 +m \angle 2 \leq 50^{\circ } + 70 ^{\circ }$

$105 ^{\circ }\leq m \angle 3 \leq 120^{\circ }$

Therefore, the measure of $\angle 3$ must fall in that range. Of the given choices, only $110^{\circ }$ falls in that range.

Report an Error

Example Question #224 : Geometry

Triangle

Refer to the above diagram.

$45^{\circ } \leq m \angle 1 \leq 50^{\circ }$

$130^{\circ } \leq m \angle 3 \leq 140 ^{\circ }$

Which of the following could be a measure of $\angle 2$ ?

Possible Answers:

$95 ^{\circ }$

$80 ^{\circ }$

$90 ^{\circ }$

All of the other responses are correct.

$85 ^{\circ }$

Correct answer:

All of the other responses are correct.

Explanation:

The measure of an exterior angle of a triangle is the sum of the measures of its remote interior angles, so

$\angle 3 = \angle 1 + \angle 2$

$\angle 2 = \angle 3 - \angle 1$

Therefore, the maximum value of $\angle 2$ is the least possible value of $\angle 1$ subtracted from the greatest possible value of $\angle 3$ :

$140^{\circ } - 45^{\circ } = 95 ^{\circ }$

The minimum value of $\angle 2$ is the greatest possible value of $\angle 1$ subtracted from the least possible value of $\angle 3$ :

$130^{\circ } - 50^{\circ } = 80 ^{\circ }$

Therefore,

$80^{\circ } \leq \angle 2 \leq 95^{\circ }$

Since all of the choices fall in this range, all are possible measures of $\angle 2$ .

Report an Error

Example Question #14 : Acute / Obtuse Triangles

Find the angle measurement of .

Possible Answers:

112

102

Correct answer:

102

Explanation:

All the angles in a triangle must add up to 180 .

32+46+y=180

78+y=180

y=102

Report an Error

Example Question #111 : Properties Of Triangles

Find the angle measurement of .

Possible Answers:

100

110

120

Correct answer:

110

Explanation:

All the angles in a triangle must add up to 180.

a+35+35=180

a+70=180

a=110

Report an Error

Example Question #112 : Properties Of Triangles

Find the angle measurement of .

Possible Answers:

115

105

Correct answer:

115

Explanation:

All the angles in a triangle must add up to 180 .

b+28+37=180

b+65=180

b=115

Report an Error

Example Question #113 : Properties Of Triangles

An isosceles triangle has an angle whose measure is $70^{\circ }$ .

What could be the measures of one of its other angles?

(a) $40^{\circ }$

(b) $55^{\circ }$

Possible Answers:

(a) or (c) only

(b) only

(a) only

(a), (b), or (c)

Correct answer:

(a), (b), or (c)

Explanation:

By the Isosceles Triangle Theorem, an isosceles triangle has two congruent interior angles. There are two possible scenarios if one angle has measure $70^{\circ }$ :

Scenario 1: The other two angles are congruent to each other. The degree measures of the interior angles of a triangle total $180^{\circ }$ , so if we let be the common measure of those angles:

x + x + 70 = 180

2x+70 = 180

2x= 110

x = 55

This makes (b) a possible answer.

Scenario 2: One of the other angles measures $70^{\circ }$ also, making (c) a possible answer. The degree measure of the third angle is

180 - (70 + 70) = 180 - 140 = 40 ,

making (a) a possible answer. Therefore, the correct choice is (a), (b), or (c).

Report an Error

Example Question #114 : Properties Of Triangles

One of the interior angles of a scalene triangle measures $54^{\circ }$ . Which of the following could be the measure of another of its interior angles?

Possible Answers:

$126^{\circ }$

$72^{\circ }$

$54^{\circ }$

$108^{\circ }$

$63^{\circ }$

Correct answer:

$108^{\circ }$

Explanation:

A scalene triangle has three sides of different measure, so, by way of the Converse of the Isosceles Triangle Theorem, each angle is of different measure as well. We can therefore eliminate $54^{\circ }$ immediately.

Also, if the triangle also has a $72^{\circ }$ angle, then, since the total of the degree measures of the angles is $180^{\circ }$ , it follows that the third angle has measure

$180 - (54+72) = 180 - 126 = 54 ^{\circ }$ .

Therefore, the triangle has two angles that measure the same, and $72^{\circ }$ can be eliminated.

Similarly, if the triangle also has a $63^{\circ }$ angle, then, since the total of the degree measures of the angles is $180^{\circ }$ , it follows that the third angle has measure

$180 - (54+63) = 180 - 117= 63 ^{\circ }$ .

The triangle has two angles that measure $63^{\circ }$ . This choice can be eliminated.

$126^{\circ }$ can be eliminated, since the third angle would have measure

$180 - (54+126) = 180 - 180= 0^{\circ }$ ,

an impossible situation since angle measures must be positive.

The remaining possibility is $108^{\circ }$ . This would mean that the third angle has measure

$180 - (54+108) = 180 - 162= 18^{\circ }$ .

The three angles have different measures, so the triangle is scalene. $108^{\circ }$ is the correct choice.

Report an Error

Example Question #5 : How To Find An Angle In An Acute / Obtuse Triangle

Given: $\bigtriangleup ABC$ with $m \angle A = 20^{\circ }, m \angle B = 32^{\circ }$ . Locate on $\overline{AB}$ so that $\overrightarrow{CD}$ is the angle bisector of $\angle ACB$ . What is $m \angle CDB$ ?

Possible Answers:

$74^{\circ }$

$79^{\circ }$

$84^{\circ }$

$69^{\circ }$

$89^{\circ }$

Correct answer:

$84^{\circ }$

Explanation:

Angle bisector

Above is the figure described.

The measures of the interior angles of a triangle total $180^{\circ }$ , so the measure of $\angle ACB$ is

$m \angle ACB = 180^{\circ } -( m \angle A + m \angle B)$

$= 180^{\circ } -( 20^{\circ } + 32^{\circ })$

$= 180^{\circ } - 52^{\circ }$

$= 128^{\circ }$

Since $\overrightarrow{CD}$ bisects this angle,

$m \angle BCD= \frac{1}{2}m \angle ACB = \frac{1}{2} \cdot 128^{\circ } =64^{\circ }$

and

$m \angle CDB = 180^{\circ } -( m \angle BCD + m \angle B)$

$= 180^{\circ } -( 64 ^{\circ } + 32^{\circ } )$

$= 180^{\circ } -96^{\circ }$

$= 84^{\circ }$

Report an Error

View SSAT- Upper Level Tutors

Christie
Certified Tutor

Elizabeth City State University, Bachelor of Education, Education. Gardner-Webb University, Masters in Education, Educational...

View SSAT- Upper Level Tutors

Errin
Certified Tutor

Converse College, Current Undergrad Student, Business Administration and Management.

View SSAT- Upper Level Tutors

Matthew
Certified Tutor

The New School, Master of Philosophy, Philosophy.

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GRE Tutors in Seattle, GMAT Tutors in Philadelphia, Calculus Tutors in San Francisco-Bay Area, French Tutors in Houston, Physics Tutors in Denver, Math Tutors in Chicago, ISEE Tutors in San Francisco-Bay Area, Reading Tutors in Philadelphia, Statistics Tutors in Houston, Spanish Tutors in Chicago

Popular Courses & Classes

MCAT Courses & Classes in Philadelphia, GMAT Courses & Classes in Dallas Fort Worth, SSAT Courses & Classes in Seattle, LSAT Courses & Classes in New York City, LSAT Courses & Classes in San Diego, GMAT Courses & Classes in Miami, ACT Courses & Classes in Houston, ISEE Courses & Classes in Chicago, SSAT Courses & Classes in Boston, GRE Courses & Classes in New York City

Popular Test Prep

ACT Test Prep in Houston, SAT Test Prep in Dallas Fort Worth, SAT Test Prep in San Diego, SSAT Test Prep in Seattle, SSAT Test Prep in Los Angeles, ISEE Test Prep in Chicago, MCAT Test Prep in Washington DC, GRE Test Prep in Miami, GRE Test Prep in Boston, GMAT Test Prep in Dallas Fort Worth

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #12 : Acute / Obtuse Triangles

Example Question #223 : Geometry

Example Question #13 : Acute / Obtuse Triangles

Example Question #224 : Geometry

Example Question #14 : Acute / Obtuse Triangles

Example Question #111 : Properties Of Triangles

Example Question #112 : Properties Of Triangles

Example Question #113 : Properties Of Triangles

Example Question #114 : Properties Of Triangles

Example Question #5 : How To Find An Angle In An Acute / Obtuse Triangle

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: