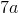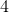We are open Saturday and Sunday!

Call Now to Set Up Tutoring:

(888) 888-0446

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

Create An Account

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #21 : Acute / Obtuse Triangles

Given: $\bigtriangleup ABC$ with $m \angle B = 74^{\circ }$ . is located on $\overline{AB}$ so that $\overrightarrow{CD}$ bisects $\angleACB$ $\angle ACB$ and forms isosceles triangle $\bigtriangleup BCD$ .

Give the measure of $\angle A$ .

Possible Answers:

$64^{\circ }$

Insufficient information is given to answer the question.

$42^{\circ }$

$74^{\circ }$

$53^{\circ }$

Correct answer:

$42^{\circ }$

Explanation:

If $\bigtriangleup BCD$ is isosceles, then by the Isosceles Triangle Theorem, two of its angles must be congruent.

Case 1: $m \angle B = m \angle BCD= 74^{\circ }$

Since $\overrightarrow{CD}$ bisects $\angleACB$ $\angle ACB$ into two congruent angles, one of which must be $m \angle BCD$ ,

$m \angle ACB = 2 \cdot m \angle BCD = 2 \cdot 74^{\circ } = 148^{\circ }$

However, this is impossible, since $\angle ACB$ and $\angle B$ are two angles of the original triangle; their total measure is

$m \angle ACB+ m \angle B = 148^{\circ }+ 74 ^{\circ } = 222 ^{\circ } > 180 ^{\circ }$

Case 2: $m \angle B = m \angle BDC= 74^{\circ }$

Then, since the degree measures of the interior angles of a triangle total $180^{\circ }$ ,

$m \angle BCD= 180^{\circ } - ( \angle B + m \angle BDC )$

$= 180^{\circ } - (74^{\circ } + 74^{\circ } )$

$= 180 ^{\circ } - 148^{\circ }$

$= 32^{\circ }$

Since $\overrightarrow{CD}$ bisects $\angleACB$ $\angle ACB$ into two congruent angles, one of which must be $m \angle BCD$ ,

$m \angle ACB = 2 \cdot m \angle BCD = 2 \cdot 32^{\circ } = 64^{\circ }$

and

$m \angle A = 180^{\circ } - ( \angle B + m \angle ACB )$

$= 180^{\circ } - (74^{\circ } + 64^{\circ } )$

$= 180^{\circ } - 138^{\circ }$

$= 42^{\circ }$

Case 3: $m \angle BDC= m \angle BCD$

Then

$m \angle B = 180^{\circ } -(m \angle BDC+ m \angle BCD)$

$74= 180^{\circ } -(m \angle BCD+ m \angle BCD)$

$74= 180^{\circ } -2 \cdot m \angle BCD$

$2 \cdot m \angle BCD = 106^{\circ }$

$m \angle BCD = 53^{\circ }$

$m \angle ACB = 2 \cdot m \angle BCD = 2 \cdot 53^{\circ } = 106^{\circ }$

$m \angle A = 180^{\circ } - ( \angle B + m \angle ACB )$

$= 180^{\circ } - ( 74^{\circ }+ 106^{\circ } )$

$= 0^{\circ }$ , which is not possible.

Therefore, the only possible measure of $\angle A$ is $42^{\circ }$ .

Report an Error

Example Question #111 : Properties Of Triangles

The interior angles of a triangle measure $x^{\circ } , \left ( x+ 26\right )^{\circ } , \left (2x+ 1\right )^{\circ }$ . Of these three degree measures, give the greatest.

Possible Answers:

$64\frac{1}{4} ^{\circ }$

This triangle cannot exist.

$77^{\circ }$

$77\frac{1}{2} ^{\circ }$

$103^{\circ }$

Correct answer:

$77\frac{1}{2} ^{\circ }$

Explanation:

The degree measures of the interior angles of a triangle total 180 degrees, so

x + (x+26) + (2x+ 1) = 180

x +x+ 2x + 26 + 1 = 180

4x+27 = 180

4x+27 - 27 = 180 - 27

4x = 153

$\frac{4x}{4} = \frac{153}{4}$

$x = 38 \frac{1}{4}$

One angle measures $38\frac{1}{4}^{\circ }$

The other two angles measure

$x+ 26 = 38\frac{1}{4} + 26 = 64\frac{1}{4} ^{\circ }$

and

$2x+ 1 = 2 \left$38\frac{1}{4}\right$+ 1 = 77 \frac{1}{2} ^{\circ }$ .

We want the greatest of the three, or $77 \frac{1}{2} ^{\circ }$ .

Report an Error

Example Question #23 : Acute / Obtuse Triangles

$\bigtriangleup ABC$ is a right triangle with right angle $\angle A$ . is located on $\overline{AB}$ so that, when $\overline{CD}$ is constructed, isosceles triangles $\bigtriangleup ADC$ and $\bigtriangleup BDC$ are formed.

What is the measure of $\angle B$ ?

Possible Answers:

$67\frac{1}{2}^{\circ }$

$30^{\circ }$

$45^{\circ }$

$15^{\circ }$

$22\frac{1}{2}^{\circ }$

Correct answer:

$22\frac{1}{2}^{\circ }$

Explanation:

The figure referenced is below:

Right triangles

Since $\bigtriangleup ADC$ is an isosceles right triangle, its acute angles - in particular, $\angle ADC$ - measure $45^{\circ }$ each. Since this angle forms a linear pair with $\angle CDB$ :

$m \angle CDB = 180^{\circ } - m \angle ADC = 180^{\circ } - 45 ^{\circ } = 135^{\circ }$ .

$\bigtriangleup BDC$ is also isosceles, so, by the Isosceles Triangle Theorem, it has two congruent angles. Since $\angle CDB$ is obtuse, and no triangle has two obtuse angles:

$m \angle BCD = m \angle B$ .

Also, $\angle ADC$ is an exterior angle of $\bigtriangleup BDC$ , whose measure is equal to the sum of those of its two remote interior angles, which are the congruent angles $m \angle BCD = m \angle B$ . Therefore,

$m \angle ADC = m \angle BCD + m \angle B$

$45^{\circ }= m \angle B + m \angle B$

$45^{\circ }=2 m \angle B$

$m \angle B = 22\frac{1}{2}^{\circ }$

Report an Error

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

The perimeter of a triangle is 18a . If one side has the length , and another side has the length , what is the length of the third side?

Possible Answers:

Correct answer:

Explanation:

The perimeter is the length of all the sides added up.

$\text{Perimeter}=\text{side 1 + side 2 + side 3}$

Using the information given in the question,

$18a=8a+6a+\text{side 3}$

Now, solve for side 3.

$\text{Side 3}=18a-8a-6a=4a$

Report an Error

Example Question #2 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

If the perimeter of the triangle is and two of the sides are given in the figure below, what is the length of the third side?

Possible Answers:

Correct answer:

Explanation:

To find the perimeter of a triangle, add up all of its sides.

Let be the length of the third side.

12+10+x=35

22+x=35

x=13

The length of the third side is .

Report an Error

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

The perimeter of the triangle is , and two of the sides are already given. What is the length of the third side?

Possible Answers:

Correct answer:

Explanation:

Add up all the sides to find the perimeter of the triangle.

Let be the length of the third side.

15+20+x=50

35+x=50

x=15

The length of the third side is .

Report an Error

Example Question #2 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

The perimeter of the triangle is , and two of the sides are already given. What is the length of the third side?

Possible Answers:

Correct answer:

Explanation:

Add up all the sides to find the perimeter of the triangle.

Let be the length of the third side.

8+9+x=27

17+x=27

x=10

The length of the third side is .

Report an Error

Example Question #3 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

The perimeter of the triangle is , and two of the sides are given. What is the length of the third side?

Possible Answers:

Correct answer:

Explanation:

Add up all the sides to find the perimeter of the triangle.

Let be the length of the third side.

5+10+x=21

15+x=21

x=6

The length of the third side is .

Report an Error

Example Question #4 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

The perimeter of the triangle is , and two of the sides are given. Find the length of the third side.

Possible Answers:

Correct answer:

Explanation:

Add up all the sides to find the perimeter of the triangle.

Let be the length of the third side.

9+12+x=36

21+x=36

x=15

The length of the third side is .

Report an Error

Example Question #5 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

A triangle with a perimeter of has side lengths of $2x-1, 3x-4, \text{ and }x$ . Find the length of the longest side.

Possible Answers:

Correct answer:

Explanation:

Add up all the sides to find the perimeter.

2x-1+3x-4+x=25

6x-5=25

6x=30

x=5

Now, plug in the value of to find the lengths of the triangle, then choose the largest one.

2x-1=2(5)-1=9

x=5

3x-4=3(5)-4=15-5=11

Report an Error

View SSAT- Upper Level Tutors

Robert
Certified Tutor

University of North Carolina at Chapel Hill, Bachelor in Arts, English. North Carolina Central University, Master of Arts, En...

View SSAT- Upper Level Tutors

Brandon
Certified Tutor

Flager College, Bachelor, Elementary Education .

View SSAT- Upper Level Tutors

Gregory
Certified Tutor

Pennsylvania State University-Main Campus, Bachelor of Science, Chemical Engineering. Carnegie Mellon University, Doctor of P...

All SSAT Upper Level Math Resources

6 Diagnostic Tests 311 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Calculus Tutors in Atlanta, Biology Tutors in Seattle, French Tutors in Seattle, GMAT Tutors in Phoenix, Chemistry Tutors in Los Angeles, GMAT Tutors in Dallas Fort Worth, Spanish Tutors in Miami, MCAT Tutors in Seattle, Statistics Tutors in Los Angeles, Chemistry Tutors in Phoenix

Popular Courses & Classes

LSAT Courses & Classes in Houston, ISEE Courses & Classes in Dallas Fort Worth, ISEE Courses & Classes in San Diego, SSAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Washington DC, GMAT Courses & Classes in Dallas Fort Worth, Spanish Courses & Classes in Philadelphia, SSAT Courses & Classes in San Diego, LSAT Courses & Classes in Chicago, Spanish Courses & Classes in Los Angeles

Popular Test Prep

LSAT Test Prep in San Francisco-Bay Area, MCAT Test Prep in Denver, GMAT Test Prep in Boston, GRE Test Prep in Denver, GMAT Test Prep in Dallas Fort Worth, GRE Test Prep in San Diego, MCAT Test Prep in Atlanta, SSAT Test Prep in San Diego, MCAT Test Prep in New York City, MCAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SSAT Upper Level Math : SSAT Upper Level Quantitative (Math)

Study concepts, example questions & explanations for SSAT Upper Level Math

All SSAT Upper Level Math Resources

Example Questions

Example Question #21 : Acute / Obtuse Triangles

Example Question #111 : Properties Of Triangles

Example Question #23 : Acute / Obtuse Triangles

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Example Question #2 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Example Question #1 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Example Question #2 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Example Question #3 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Example Question #4 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

Example Question #5 : How To Find The Length Of The Side Of An Acute / Obtuse Triangle

All SSAT Upper Level Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: