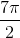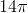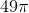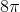The formula for the area of a circle is as follows:

In this formula, A is area, and r is for radius. We know the diameter of the circle is 6, meaning we have to first find the radius. The diameter is twice the length of the radius of a circle, meaning to find radius divide the diameter by 2:

Now plug in the numbers to get the answer. Since pi is an irrational constant, it is okay to leave the answer in terms of pi.

The formula for the area of a circle is as follows:

In this formula, A is area, and r is for radius. We know the diameter of the circle is 16, meaning we have to first find the radius. The diameter is twice the length of the radius of a circle, meaning to find radius divide the diameter by 2:

Now plug in the numbers to get the answer. Since pi is an irrational constant, it is okay to leave the answer in terms of pi.

The equation of a circle on the coordinate plane is 

where  is the radius. Therefore, 

and 

.

The circumference of a circle is  times is radius, which here would be 

The figure is a sector of a circle with radius 8; the sector has degree measure . The length of the arc is 

The equation of a circle on the coordinate plane is 

,

where  is the radius. Therefore, 

and 

.

The circumference of a circle is  times is radius, which here would be

.

The figure below shows , which matches this description, along with its chord  and triangle bisector . 

We will concentrate on , which is a 30-60-90 triangle.

Chord  has length 24, so  has length half this, or 12.

By the 30-60-90 Theorem, 

and 

This is the radius, so the circumference is

If a (perpendicular) radius of the inscribed circle is constructed to the triangle, and a radius of the circumscribed circle is constructed to a neighboring vertex, a right triangle is formed. By symmetry, it can be shown that this is a 30-60-90 triangle, and, subsequently,

If we let , the circumference of the inscribed circle is .

Then , and the circumference of the circumscribed circle is .

The ratio of the circumferences is therefore 2 to 1.

If a right triangle is inscribed inside a circle, then the arc intercepted by the right angle is a semicircle, making the hypotenuse of triangle a diameter. 

The length of the hypotenuse of this triangle can be calculated using the Pythagorean Theorem:

This is the diameter, also, so the circumference is .

If a right triangle is inscribed inside a circle, then the arc intercepted by the right angle is a semicircle, making the hypotenuse of triangle a diameter. 

The length of the shorter leg of a 30-60-90 triangle is that of the longer leg divided by , so the shorter leg will have length

The hypotenuse will have length twice that of its short leg, so the hypotenuse of this triangle will have twice this length, or 

This is the diameter, so multiply this by  to get the circumference:

An equilateral triangle of perimeter 60 has sidelength one-third of this, or 20. 

Construct this triangle and its inscribed circle, as well as a radius to one side - which, by symmetry, is a perpendicular bisector - and a segment to one of that side's endpoints:

Each side of the triangle has measure 20, so . Also, the triangle formed by the segments, by symmetry, is a 30-60-90 triangle. Therefore, 

which is the radius of the circle. The cricumference of the circle is  times this, or