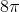You must first set up a revenue equation where  represents the number of bunches of apples sold and  represents the number of watermelons sold.  

This would give us the equation 

.  

The problem gives us both  and  and when we plug those values in we get 

or

.

Now you must get  by itself.  

First, subtract  from both sides leaving .  

Then divide both sides by  to get your answer .

To solve this algebraic word problem, first set up an equation:

The variable  represents the amount of people in the group.

Add 

Isolate the variable by adding 8 to both sides of the equation:

Check to make sure that the two conditions of the problem have been met.

Condition one: The two numbers added together must equal 60.

Condition two. One of the numbers is eight less than the other.

Because these two conditions have been met, there are  people in one group and  people in the second group.

The formula for computing the area of a rectangle is Area = l x w, where l = length and w = width.

In this algebraic word problem, let the variable  represent the length and  will represent the width of the rectangle.

Write an equation:

Distribute the variable  to what is inside the parentheses:

Set that expression equal to zero by subtracting 36 from both sides:

Factor using the FOIL Method:

Set each equal to zero to find the values of x that make this expression true:

There are two possible values for ;  and 

Because a dimension cannot be a negative integer, reject  Therefore . This is the measurement of the length of the rectangle.

 represents the width of the rectangle.

Now check to see if the two conditions are met.

Condition 1: Area = length x width

Condition 2: The width is 5cm less than the length.

Therefore  is the length and  is the width of this rectangle.

The figure is a sector of a circle with radius 8; the sector has degree measure . The area of the sector is 

The figure is a semicircle - one-half of a circle - with radius 5.5, or . Its area is one-half of the square of the radius multiplied by  - that is, 

The equation of a circle on the coordinate plane is 

,

where  is the radius. Therefore, in this equation, 

.

The area of a circle is found using the formula

,

so we substitute 66 for , yielding

.

If a right triangle is inscribed inside a circle, then the arc intercepted by the right angle is a semicircle, making the hypotenuse of triangle a diameter. 

The length of a hypotenuse of a 30-60-90 triangle is twice that of its short leg, so the hypotenuse of this triangle will be twice 11, or 22. The diameter of the circle is therefore 22, and the radius is half this, or 11. The area of the circle is therefore

Examine the following diagram:

If a (perpendicular) radius of the inscribed circle is constructed to the triangle, and a radius of the circumscribed circle is constructed to a neighboring vertex, a right triangle is formed. By symmetry, it can be shown that this is a 30-60-90 triangle, and, subsequently,

If we let , the area of the inscribed circle is .

Then , and the area of the circumscribed circle is  

The ratio of the areas is therefore 4 to 1.

An equilateral triangle of perimeter 54 has sidelength one-third of this, or 18. 

Construct this triangle and its circumscribed circle, as well as a perpendicular bisector to one side and a radius to one of that side's endpoints:

Each side of the triangle has measure 18, so . Also, the triangle formed by the segments, by symmetry, is a 30-60-90 triangle. By the 30-60-90 Theorem, 

and .

The latter is the radius, so the area of this circle is 

The figure below shows , which matches this description, along with its chord :

By way of the Isosceles Triangle Theorem,  can be proved equilateral, so . This is the radius, so the area is