All SSAT Upper Level Math Resources
Example Questions
Example Question #6 : How To Find The Area Of A Pentagon
A regular pentagon has an area of 

To find the area of a regular polygon,
For the given pentagon,
To find the length of each side of the pentagon, divide the perimeter by 
Example Question #7 : How To Find The Area Of A Pentagon
The area of a regular pentagon is 

To find the area of a regular polygon,
For the given pentagon,
To find the length of each side of the pentagon, divide the perimeter by 
Example Question #31 : Areas And Perimeters Of Polygons
Find the area of a regular pentagon that has a side length of 

To find the area of a regular polygon,
To find the perimeter of the pentagon,
For the given pentagon,
So then, to find the area of the pentagon,
Example Question #11 : How To Find The Area Of A Pentagon
Find the area of a regular pentagon that has a side length of 

To find the area of a regular polygon,
To find the perimeter of the pentagon,
For the given pentagon,
So then, to find the area of the pentagon,
Example Question #12 : How To Find The Area Of A Pentagon
Find the area of a regular pentagon with a side length of 

To find the area of a regular polygon,
To find the perimeter of the pentagon,
For the given pentagon,
So then, to find the area of the pentagon,
Example Question #1 : How To Find The Area Of A Square
The volume of a cube is 1,000 cubic centimeters. Using the conversion factor 2.5 centimeters = 1 inch, give its surface area in square inches, rounding to the nearest square inch.
144 square inches
75 square inches
100 square inches
108 square inches
96 square inches
96 square inches
The surface area of a cube is six times the square of its sidelength, so we find the sidelength. This is the cube root of volume 1,000, so
![\sqrt[3]{1000}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/106684/gif.latex)

To rewrite this as inches, divide by 2.5:




The surface area of the cube in square inches is



Example Question #1 : How To Find The Area Of A Square
The volume of a cube is 64 cubic inches. Find the side length of the cube and its surface area.
The volume of a cube is 


A cube has six faces and the surface area of a cube is 
Surface area =
Example Question #51 : Areas And Perimeters Of Polygons
A square has an area of 16 square inches. Give the diagonal of the square.
In order to determine the length of the diagonal of a square we would use the Pythagorean Theorem. First we should find the side length:

Now, "square" the length of one side and multiply by 2, then take the square root of that number to get the length of the diagonal:
Example Question #3 : How To Find The Area Of A Square
John is going to apply a fertilizer to his farm which has a dimension of 200 feet by 200 feet. Every pound of the fertilizer that he is going to use is sufficient for 40 square feet. If the fertilizer costs 2 dollars per pound, how much he should spend to fertilize his farm?
The area of the farm is:


Every pound of the fertilizer costs $2, so he needs to spend 
Example Question #2 : How To Find The Area Of A Square
The diagonal length of a square is 

We need to use the Pythagorean Theorem in order to solve this problem. We can write:

where 


All SSAT Upper Level Math Resources



























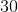




















![Volume=64\Rightarrow s=\sqrt[3]{64}=4\ in](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/147617/gif.latex)





















