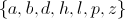All SSAT Middle Level Math Resources
Example Questions
Example Question #3 : Find Range
Given the following set of numbers, find the range.
In order to find the range for a set of data, take the largest number and subtract the smallest number.
In this case, the largest number is 

Remember that when we subtract a negative, we are actually adding the absolute value of the numbers:
Therefore:


Example Question #2 : Range
Use the following data set to answer the question:
Find the range.
To find the range, we will find the smallest number and the largest number. Then, we will find the difference of those two numbers.
So, given the set
we can see the smallest number is 2 and the largest number is 10. Now, we will find the difference. We get
Therefore, the range of the data set is 8.
Example Question #141 : Data Analysis
Mrs. Swavorski recently gave an English test to her class of 15 students. The test scores are shown below:
What is the range of the test scores listed?
A range is simply the highest score minus the lowest score.
The highest score was 

Example Question #161 : Data Analysis And Probability
Define two sets as follows:
Which of the following is a subset of 
Each of the sets listed is a subset of 



A set is a subset of 







Example Question #1 : Sets
Define two sets as follows:
Which of the following numbers is an element of 










425 and 565 are not multiples of 9; neither is in 




Example Question #1 : How To Find The Missing Part Of A List
Complete the set by determining the value of 
The set is composed of consecutive squares.
We can see that 
Therefore, 36 is the correct answer.
Example Question #2 : How To Find The Missing Part Of A List
Define sets 


How many elements are in the set 
Two
Four
One
Three
The correct answer is not given among the other responses.
The correct answer is not given among the other responses.
The elements of the set 







Example Question #3 : How To Find The Missing Part Of A List
Which of the following is a subset of the set

For a set to be a subset of 


We can do that with four choices:




However, the remaining set, 

Example Question #1 : Sets
Define sets 


How many elements are in the set 
Three
The correct answer is not given among the other responses.
One
Two
None
Three
The elements of the set 




Example Question #1 : How To Find The Missing Part Of A List
Which of the following is a subset of the set

The correct answer is not among the answer choices.
The correct answer is not among the answer choices.
We show that none of the four listed sets can be a subset of the primes by identifying one composite number in each - that is, by proving that there is at least one factor not equal to 1 or itself:




Since each set has at least one element that is not a prime, each has at least one element not in 

Certified Tutor
All SSAT Middle Level Math Resources