$\displaystyle \frac{4}6{+\frac{3}{8}}$

In order to solve this problem, we first have to find common denominators. 

$\displaystyle \frac{4}{6}\times\frac{4}{4}=\frac{16}{24}$

$\displaystyle \frac{3}{8}\times\frac{3}{3}=\frac{9}{24}$

Now that we have common denominators, we can add the fractions. Remember, when we add and subtract fractions, we only add or subtract the numerator. 

$\displaystyle \frac{16}{24}+\frac{9}{24}=\frac{25}{24}$

$\displaystyle \frac{25}{24}=1\frac{1}{24}$ because $\displaystyle 24$ can go into $\displaystyle 25$ one time with $\displaystyle 1$ left over. 

$\displaystyle 3+7=10$

If we count all the squares together we have $\displaystyle 10$ squares. 

In this series we are counting by $\displaystyle 100$. When counting by $\displaystyle 100$, $\displaystyle 900$ is between $\displaystyle 800$ and $\displaystyle 1\textup,000$.

The commutative property says that you can add the numbers in any order and still get the same answer. $\displaystyle 3+2$ and $\displaystyle 2+3$ both equal $\displaystyle 5$. 

This is an addition problem because we want to know how much total time Joe spent cleaning all together. We can add the numbers in any order, $\displaystyle 50+17+22=89.$

$\displaystyle \frac{7}8{+\frac{2}{4}}$

In order to solve this problem, we first have to find common denominators. $\displaystyle \frac{2}{4}\times\frac{2}{2}=\frac{4}{8}$

Now that we have common denominators, we can add the fractions. Remember, when we add and subtract fractions, we only add or subtract the numerator. 

$\displaystyle \frac{7}{8}+\frac{4}{8}=\frac{11}{8}$

$\displaystyle \frac{11}{8}=1\frac{3}{8}$ because $\displaystyle 8$ can go into $\displaystyle 11$ one time with $\displaystyle 3$ left over. 

$\displaystyle \frac{3}{5}+\frac{1}3$

In order to solve this problem, we first have to find common denominators. 

$\displaystyle \frac{3}5{} \times\frac{3}{3}=\frac{9}{15}$

$\displaystyle \frac{1}{3}\times\frac{5}{5}=\frac{5}{15}$

Now that we have common denominators, we can add the fractions. Remember, when we add and subtract fractions, we only add or subtract the numerator. 

$\displaystyle \frac{9}{15}+\frac{5}{15}=\frac{14}{15}$

When adding any number by $\displaystyle 10$ the only number that will change in your answer is the tens place. 

$\displaystyle 6+0=6$

$\displaystyle 8+1=9$

$\displaystyle 2+0=2$

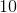
$\displaystyle \frac{\begin{array}[b]{r}286\\ +\ 10\end{array}}{\ \ \space296}$

$\displaystyle 2+8=10$, so we need to add $\displaystyle 8$ more triangles to the $\displaystyle 2$ triangles to have $\displaystyle 10.$

$\displaystyle 2+1=3$ and $\displaystyle 3+0=3$ both equal $\displaystyle 3$ so they are equal.