All SSAT Elementary Level Math Resources
Example Questions
Example Question #261 : Understanding Addition And Subtraction
Use the triangles ![]() below to help you answer the subtraction problem.
below to help you answer the subtraction problem.

We have 






Example Question #251 : Understanding Addition And Subtraction
Use the triangles ![]() below to help you answer the subtraction problem.
below to help you answer the subtraction problem.

We have 






Example Question #71 : Knowing How To Subtract
Use the triangles ![]() below to help you answer the subtraction problem.
below to help you answer the subtraction problem.

We have 






Example Question #451 : How To Subtract
Find the difference between 

To find the difference, you need to subtract. When subtracting, always remember to put the greater number first!
When we try to subtract the ones place, we will need to cancel. For 22, the ones place becomes 12 and the tens place becomes 1.
The difference between 14 and 22 is 8.
Example Question #451 : How To Subtract
Lucy bought a t-shirt and jeans from the store. With tax, she spent 

To find the difference, you must subtract. Line up the numbers vertically. Remember to use the rules of borrowing to subtract:
Lucy got 
Example Question #451 : How To Subtract

To find the missing piece of an addition problem, we can take the biggest number minus the smallest number.
We can start at 

Example Question #452 : How To Subtract

To find the missing piece of an addition problem, we can take the biggest number minus the smallest number.
We can start at 

Example Question #453 : How To Subtract

To find the missing piece of an addition problem, we can take the biggest number minus the smallest number.
We can start at 

Example Question #454 : How To Subtract

To find the missing piece of an addition problem, we can take the biggest number minus the smallest number.
We can start at 

Example Question #455 : How To Subtract

To find the missing piece of an addition problem, we can take the biggest number minus the smallest number.
We can start at 

Certified Tutor
Certified Tutor
All SSAT Elementary Level Math Resources




















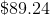








![\frac{\begin{array}[b]{r}11\\ -\ 10\end{array}}{ \ \ \ \ \ \space 1}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/523090/gif.latex)





![\frac{\begin{array}[b]{r}12\\ -\ 10\end{array}}{ \ \ \ \ \ \space 2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/523111/gif.latex)





![\frac{\begin{array}[b]{r}13\\ -\ 10\end{array}}{ \ \ \ \ \ \space 3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/522915/gif.latex)





![\frac{\begin{array}[b]{r}14\\ -\ 10\end{array}}{ \ \ \ \ \ \space 4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/522921/gif.latex)





![\frac{\begin{array}[b]{r}15\\ -\ 10\end{array}}{ \ \ \ \ \ \space 5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/522931/gif.latex)




