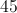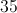All SAT Math Resources
Example Questions
Example Question #3 : How To Find An Angle In A Polygon
In triangle ABC, the measure of angle A = 70 degrees, the measure of angle B = x degrees, and the measure of angle C = y degrees. What is the value of y in terms of x?
70 – x
70 + x
x – 70
110 + x
110 – x
110 – x
Since the three angles of a triangle sum to 180, we know that 70 + x + y = 180. Subtract 70 from both sides and see that x + y = 110. Subtract x from both sides and see that y = 110 – x.
Example Question #1 : How To Find An Angle In A Polygon
What is the measure, in degrees, of each interior angle of a regular convex polygon that has twelve sides?
150
120
180
175
135
150
The sum of the interior angles, in degrees, of a regular polygon is given by the formula 180(n – 2), where n is the number of sides. The problem concerns a polygon with twelve sides, so we will let n = 12. The sum of the interior angles in this polygon would be 180(12 – 2) = 180(10) = 1800.
Because the polygon is regular (meaning its sides are all congruent), all of the angles have the same measure. Thus, if we divide the sum of the measures of the angles by the number of sides, we will have the measure of each interior angle. In short, we need to divide 1800 by 12, which gives us 150.
The answer is 150.
Example Question #5 : How To Find An Angle In A Polygon
In the figure above, polygon ABDFHGEC is a regular octagon. What is the measure, in degrees, of angle FHI?
45
50
30
60
40
45
Angle FHI is the supplement of angle FHG, which is an interior angle in the octagon. When two angles are supplementary, their sum is equal to 180 degrees. If we can find the measure of each interior angle in the octagon, then we can find the supplement of angle FHG, which will give us the measure of angle FHI.
The sum of the interior angles in a regular polygon is given by the formula 180(n – 2), where n is the number of sides in the polygon. An octagon has eight sides, so the sum of the angles of the octagon is 180(8 – 2) = 180(6) = 1080 degrees. Because the octagon is regular, all of its sides and angles are congruent. Thus, the measure of each angle is equal to the sum of its angles divided by 8. Therefore, each angle in the polygon has a measure of 1080/8 = 135 degrees. This means that angle FHG has a measure of 135 degrees.
Now that we know the measure of angle FHG, we can find the measure of FHI. The sum of the measures of FHG and FHI must be 180 degrees, because the two angles form a line and are supplementary. We can write the following equation:
Measure of FHG + measure of FHI = 180
135 + measure of FHI = 180
Subtract 135 from both sides.
Measure of FHI = 45 degrees.
The answer is 45.
Example Question #1 : How To Find An Angle In A Polygon
What is the measure of each angle in a regular octagon?
An octagon contains six triangles, or 1080 degrees. This means with 8 angles, each angle is 135 degrees.
Example Question #1 : Other Polygons
What is the measure of each central angle of an octagon?
There are 360 degrees and 8 angles, so dividing leaves 45 degrees per angle.
Example Question #1 : How To Find An Angle In A Polygon
What is the average (arithmetic mean) of all 15 interior angles of a quadrilateral, pentagon, and hexagon?
The 4 angles of a quadrilateral add to 360
The 5 angles of a pentagon add to 540
The 6 angles of a hexagon add to 720
Example Question #2 : How To Find An Angle In A Polygon
Find the sum of the interior angles in a nonagon.
To solve, simply use the formula for the total degrees in a polygon, where n is the number of vertices.
In this particular case, a nonagon is a shape with nine sides and thus nine vertices.
Thus,
Example Question #10 : How To Find An Angle In A Polygon
Which of the following cannot be the measure of an exterior angle of a regular polygon?
If one exterior angle is taken at each vertex of any convex polygon, the sum of their measures is 


Given the common measure 
Multiplying both sides by 
and
Since 



A quick check confirms that 360 divided by 8, 10, 12, or 15 yields a whole result.
Example Question #372 : Geometry
To the nearest whole degree, give the measure of each interior angle of a regular polygon with 17 sides.
The measure of each interior angle of an 
Setting 
The correct choice is therefore 
Example Question #373 : Geometry
Each interior angle of a regular polygon has measure 
The easiest way to work this is arguably to examine the exterior angles, each of which forms a linear pair with an interior angle. If an interior angle measures 
The measures of the exterior angles of a polygon, one per vertex, total 




Multiply both sides by 
The polygon has 72 vertices and, thus, 72 sides.
Certified Tutor
Certified Tutor
All SAT Math Resources