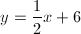Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #1 : How To Find The Equation Of A Parallel Line

There is a line defined by the equation below:

3x+4y=12

There is a second line that passes through the point (1,2) and is parallel to the line given above. What is the equation of this second line?

Possible Answers:

$y=\frac{3}{4}x+1.25$

$y=\frac{3}{4}x+2.625$

$y=-\frac{3}{4}x+1.25$

$y=\frac{3}{4}x+2.75$

$y=-\frac{3}{4}x+2.75$

Correct answer:

$y=-\frac{3}{4}x+2.75$

Explanation:

Parallel lines have the same slope. Solve for the slope in the first line by converting the equation to slope-intercept form.

3x + 4y = 12

4y = –3x + 12

y = –(3/4)x + 3

slope = –3/4

We know that the second line will also have a slope of –3/4, and we are given the point (1,2). We can set up an equation in slope-intercept form and use these values to solve for the y-intercept.

y = mx + b

2 = –3/4(1) + b

2 = –3/4 + b

b = 2 + 3/4 = 2.75

Plug the y-intercept back into the equation to get our final answer.

y = –(3/4)x + 2.75

Report an Error

Example Question #2 : How To Find The Equation Of A Parallel Line

What is the equation of a line that is parallel to 3x + 5y = 8 and passes through (10, 4) ?

Possible Answers:

$y=\frac{3}{4}x-2$

$y=\frac{5}{6}x-10$

$y=\frac{3}{8}x-5$

$y=-\frac{3}{5}x+10$

$y=\frac{5}{3}x+5$

Correct answer:

$y=-\frac{3}{5}x+10$

Explanation:

To solve, we will need to find the slope of the line. We know that it is parallel to the line given by the equation, meaning that the two lines will have equal slopes. Find the slope of the given line by converting the equation to slope-intercept form.

3x + 5y = 8

5y=-3x+8

$y=-\frac{3}{5}x+\frac{8}{5}$

The slope of the line will be $-\frac{3}{5}$ . In slope intercept-form, we know that the line will be $y=-\frac{3}{5}x+b$ . Now we can use the given point to find the y-intercept.

$y=-\frac{3}{5}x+b$

$4=-\frac{3}{5}(10)+b$

4=-6+b

10=b

The final equation for the line will be $y=-\frac{3}{5}x+10$ .

Report an Error

Example Question #3 : Parallel Lines

What line is parallel to 3x + 2y = 6 and passes through the point (2,-1) ?

Possible Answers:

$y = \frac{-1}{3}x - 5$

$y = \frac{-3}{2}x + 2$

y = 3x - 15

$y = \frac{1}{3}x + 6$

$y = \frac{2}{3}x - 3$

Correct answer:

$y = \frac{-3}{2}x + 2$

Explanation:

Start by converting the original equation to slop-intercept form.

3x + 2y = 6

2y=-3x+6

$y=-\frac{3}{2}+3$

The slope of this line is $-\frac{3}{2}$ . A parallel line will have the same slope. Now that we know the slope of our new line, we can use slope-intercept form and the given point to solve for the y-intercept.

$y=-\frac{3}{2}x+b$

$-1=-\frac{3}{2}(2)+b$

-1=-3+b

b=2

Plug the y-intercept into the slope-intercept equation to get the final answer.

$y=-\frac{3}{2}x+2$

Report an Error

Example Question #1 : Parallel Lines

What is the equation of a line that is parallel to the line $\small y=\frac{1}{2}x+3$ and includes the point (4, 2) ?

Possible Answers:

$\small y=\frac{1}{2}x+6$

$\small y=-2x+10$

$\small y=2x-6$

$\small y=\frac{1}{2}x$

Correct answer:

$\small y=\frac{1}{2}x$

Explanation:

The line parallel to $\small y=\frac{1}{2}x+3$ must have a slope of $\frac{1}{2}$ , giving us the equation $\small y=\frac{1}{2}x+b$ . To solve for b, we can substitute the values for y and x.

$\small 2=(\frac{1}{2})(4)+b$

$\small 2=2+b$

$\small b=0$

Therefore, the equation of the line is $\small y=\frac{1}{2}x$ .

Report an Error

Example Question #4 : Parallel Lines

What line is parallel to 5x + 3y = 8 , and passes through the point (6,-4) ?

Possible Answers:

$y = \frac{3}{5}x - 2$

$y = \frac{1}{3}x - 3$

$y = \frac{3}{2}x - 4$

$y = \frac{-5}{3}x + 6$

$y = \frac{-2}{3}x + 5$

Correct answer:

$y = \frac{-5}{3}x + 6$

Explanation:

Converting the given line to slope-intercept form we get the following equation:

$y = \frac{-5}{3}x + \frac{8}{3}$

For parallel lines, the slopes must be equal, so the slope of the new line must also be $\frac{-5}{3}$ . We can plug the new slope and the given point into the slope-intercept form to solve for the y-intercept of the new line.

y = mx + b

$-4 = \frac{-5}{3}(6) + b$

-4=-10+b

b = 6

Use the y-intercept in the slope-intercept equation to find the final answer.

$y = \frac{-5}{3}x + 6$

Report an Error

Example Question #2 : Parallel Lines

What line is parallel to 2x+3y=6 at (3, 2) ?

Possible Answers:

$y=-\frac{2}{3}x+4$

None of the answers are correct

$y=-\frac{3}{2}x+8$

$y=-\frac{3}{2}x+4$

$y=-\frac{2}{3}x-4$

Correct answer:

$y=-\frac{2}{3}x+4$

Explanation:

Find the slope of the given line: y=mx+b (slope intercept form)

$y=\frac{-2}{3}x+2$ therefore the slope is $\frac{-2}{3}$

Parallel lines have the same slope, so now we need to find the equation of a line with slope $\frac{-2}{3}$ and going through point (3, 2) by substituting values into the point-slope formula.

$2=\frac{-2}{3}(3)+b$

So, b=4

Thus, the new equation is $y=\frac{-2}{3}x+4$

Report an Error

Example Question #1 : Parallel Lines

If the line through the points (5, –3) and (–2, p) is parallel to the line y = –2x – 3, what is the value of p ?

Possible Answers:

–10

–17

Correct answer:

Explanation:

Since the lines are parallel, the slopes must be the same. Therefore, (p+3) divided by (–2–5) must equal –2. 11 is the only choice that makes that equation true. This can be solved by setting up the equation and solving for p, or by plugging in the other answer choices for p.

$\frac{p--3}{-2-5}=\frac{p+3}{-2-5}=-2$

$\frac{p+3}{-7}=-2$

$(\frac{p+3}{-7})-7=-2(-7)$

p+3=14

p=11

Report an Error

Example Question #5 : How To Find The Equation Of A Parallel Line

Which of these formulas could be a formula for a line perpendicular to the line 2x + 3y = 16 ?

Possible Answers:

6y - 9x = 16.5

4x + 6y = 24

6y + 9x = 16

3y - 4x = 23

4y - 9x = 24

Correct answer:

6y - 9x = 16.5

Explanation:

This is a two-step problem. First, the slope of the original line needs to be found. The slope will be represented by "" when the line is in -intercept form (y=mx+b) .

2x +3y = 16

3y = -2x +16

$y = \left(\frac{-2}{3}\right)x +\left(\frac{16}{3}\right)$

So the slope of the original line is $-\frac{2}{3}$ . A line with perpendicular slope will have a slope that is the inverse reciprocal of the original. So in this case, the slope would be $\frac{3}{2}$ . The second step is finding which line will give you that slope. For the correct answer, we find the following:

6y - 9x = 16.5

6y = 9x +16.5

$y= \left(\frac{3}{2}x\right) +\left(\frac{16.5}{6}\right)$

So, the slope is $\frac{3}{2}$ , and this line is perpendicular to the original.

Report an Error

Example Question #392 : Geometry

Which of the following equations is parallel to: $y=\frac {2}{3}x+4$ and goes through the point (3,5) ?

Possible Answers:

$y=\frac {2}{3}x+3$

$y=\frac {2}{3}x-3$

3y-4x=15

y=3x

Correct answer:

$y=\frac {2}{3}x+3$

Explanation:

Step 1: We need to define what a parallel line is. A parallel line has the same slope as the line given in the problem. Parallel lines never intersect, which tells us that the y-intercepts of the two equations are different.

Step 2: We need to identify the slope of the line given to us. The slope is always located in front of the .

The slope in the equation is $\frac {2}{3}$ .

Step 3: If we said that a parallel line has the same slope as the given line in the equation, the slope of the parallel equation is also $\frac {2}{3}$ .

Step 4. We need to write the equation of the parallel line in slope-intercept form: y=mx+b . We need to write b for the intercept because it has changed.

The equation is: $y=\frac {2}{3}x+b$

Step 5: We will use the point (3,5) where x=3 and y=5 . We need to substitute these values of x and y into the equation in step 4 and find the value of b.

$y=\frac {2}{3}x+b$
$5=\frac {2}{3}*3+b$
$5=\frac {2}{{\color{Red} 3}}*{\color{Red} 3}+b$
The numbers in red will cancel out when I multiply.
5=2+b
To find b, subtract 2 to the other side
5-2=b
3=b

Step 6: We put all of the parts together and make the final equation of the parallel line:

The final equation is: $y=\frac {2}{3}x+3$

Report an Error

Example Question #391 : Sat Mathematics

Consider line c to be y= -4x - 7. Which is the reflection of line c across the x-axis?

Possible Answers:

y = –4x + 7

y = 4x – 7

y = 4x + 7

y = (1/4)x + 7

Correct answer:

y = 4x + 7

Explanation:

A line reflected across the x-axis will have the negative value of the slope and intercept. This leaves y= 4x + 7.

Report an Error

View SAT Mathematics Tutors

Stephen
Certified Tutor

Grinnell College, Bachelor in Arts, Computer Science.

View SAT Mathematics Tutors

Danielle
Certified Tutor

Penn State University, Bachelor of Science, Civil Engineering.

View SAT Mathematics Tutors

Andy
Certified Tutor

The University of Texas at Dallas, Bachelors, Interdisciplinary Studies .

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

LSAT Courses & Classes in Washington DC, GMAT Courses & Classes in Chicago, GMAT Courses & Classes in Phoenix, ACT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in San Francisco-Bay Area, GRE Courses & Classes in San Diego, Spanish Courses & Classes in Philadelphia, ACT Courses & Classes in Seattle, MCAT Courses & Classes in San Diego, SAT Courses & Classes in Dallas Fort Worth

Popular Test Prep

GMAT Test Prep in Phoenix, ACT Test Prep in Denver, ISEE Test Prep in San Diego, LSAT Test Prep in San Francisco-Bay Area, ISEE Test Prep in Seattle, ISEE Test Prep in San Francisco-Bay Area, MCAT Test Prep in New York City, ACT Test Prep in Dallas Fort Worth, LSAT Test Prep in Denver, ACT Test Prep in New York City

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : SAT Mathematics

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #1 : How To Find The Equation Of A Parallel Line

Example Question #2 : How To Find The Equation Of A Parallel Line

Example Question #3 : Parallel Lines

Example Question #1 : Parallel Lines

Example Question #4 : Parallel Lines

Example Question #2 : Parallel Lines

Example Question #1 : Parallel Lines

Example Question #5 : How To Find The Equation Of A Parallel Line

Example Question #392 : Geometry

Example Question #391 : Sat Mathematics

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: