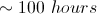Call Now to Set Up Tutoring:

(888) 888-0446

SAT Math : Circles

Study concepts, example questions & explanations for SAT Math

Create An Account

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #28 : How To Find The Area Of A Circle

An original circle has an area of $16\pi$ . If the radius is increased by a factor of 3, what is the ratio of the new area to the old area?

Possible Answers:

$10:1$

$3:1$

$9:1$

$8:1$

$7:1$

Correct answer:

$9:1$

Explanation:

The formula for the area of a circle is $\pi r^{2}$ . If we increase $r$ by a factor of 3, we will increase the area by a factor of 9.

Report an Error

Example Question #31 : Radius

A square has an area of $36\ in^{2}$ . If the side of the the square is the same as the diameter of a circle, what is the area of the circle?

Possible Answers:

$18\pi \ in^{2}$

$12\pi \ in^{2}$

$36\pi \ in^{2}$

$9\pi \ in^{2}$

$27\pi \ in^{2}$

Correct answer:

$9\pi \ in^{2}$

Explanation:

The area of a square is given by $A = s^{2}$ so we know that the side of the square is 6 in. If a circle has a diameter of 6 in, then the radius is 3 in. So the area of the circle is $A = \pi r^{2}$ or $9\pi \ in^{2}$ .

Report an Error

Example Question #32 : Radius

Mary has a decorative plate with a diameter of ten inches. She places the plate on a rectangular placemat with a length of 18 inches and a width of 12 inches. How much of the placemat is visible?

Possible Answers:

$191\pi\hspace{1 mm}inches^2$

$25\pi\hspace{1 mm}inches^2$

$216\hspace{1 mm}inches^2$

$216-25\pi\hspace{1 mm}inches^2$

$216\pi\hspace{1 mm}inches^2$

Correct answer:

$216-25\pi\hspace{1 mm}inches^2$

Explanation:

First we will calculate the total area of the placemat:

$A=l\times w= 18\times 12= 216\hspace{1 mm}inches^2$

Next we will calculate the area of the circular place

$A=\pi r^2$

And

$d=2r=10$

$r=5\hspace{1 mm}inches$

$A=\pi r^2=\pi (5^2)=25\pi\hspace{1 mm}inches^2$

We will subtract the area of the plate from the total area

$216-25\pi\hspace{1 mm}inches^2$

Report an Error

Example Question #33 : Radius

The picture above contains both a circle with diameter 4, and a rectangle with length 8 and width 5. Find the area of the shaded region. Round your answer to the nearest integer

Possible Answers:

Correct answer:

Explanation:

First, recall that the diameter of a circle is twice the value of the radius. Therefore a circle with diameter 4 has a radius of 2. Next recall that the area of a circle with radius r=2 is:

$\pi r^2 = \pi(2)^2 = 4 \pi$

The area of the rectangle is the length times the width:

$L \times W = 8 \times 5 = 40$

The area of the shaded region is the difference between the 2 areas:

$40 - 4 \pi \approx 40-4(3.14) = 27.44$

The nearest integer is 27.

Report an Error

Example Question #34 : Radius

Allen was running around the park when he lost his keys. He was running around aimlessly for the past 30 minutes. When he checked 10 minutes ago, he still had his keys. Allen guesses that he has been running at about 3m/s.

If Allen can check 1 square kilometer per hour, what is the longest it will take him to find his keys?

Possible Answers:

$\sim 100\ hours$

$\sim 3\ hours$

$\sim 81\ hours$

$\sim 10\ hours$

$\sim 1,000\ hours$

Correct answer:

$\sim 10\ hours$

Explanation:

Allen has been running for 10 minutes since he lost his keys at 3m/s. This gives us a maximum distance of 3*600=1800m from his current location. If we move 1800m in all directions, this gives us a circle with radius of 1800m. The area of this circle is

$1800^2\pi \approx 10,178,760m^2$

Our answer, however, is asked for in kilometers. 1800m=1.8km, so our actual area will be $\frac{10,178,760}{1,000,000} = 10.2$ square kilometers. Since he can search 1 per hour, it will take him at most 10.2 hours to find his keys.

Report an Error

Example Question #41 : Radius

A 12x16 rectangle is inscribed in a circle. What is the area of the circle?

Possible Answers:

100π

90π

10π

50π

120π

Correct answer:

100π

Explanation:

Explanation: Visualizing the rectangle inside the circle (corners touching the circumference of the circle and the center of the rectangle is the center of the circle) you will see that the rectangle can be divided into 8 congruent right triangles, with the hypotenuse as the radius of the circle. Calculating the radius you divide each side of the rectangle by two for the sides of each right triangle (giving 6 and 8). The hypotenuse (by pythagorean theorem or just knowing right triangle sets) the hypotenuse is give as 10. Area of a circle is given by πr². 10² is 100, so 100π is the area.

Report an Error

Example Question #42 : Radius

A circle is inscribed in a square whose side is 6 in. What is the difference in area between the square and the circle, rounded to the nearest square inch?

Possible Answers:

$11\ in^{2}$

$8\ in^{2}$

$4\ in^{2}$

$12\ in^{2}$

$14\ in^{2}$

Correct answer:

$8\ in^{2}$

Explanation:

The circle is inscribed in a square when it is drawn within the square so as to touch in as many places as possible. This means that the side of the square is the same as the diameter of the circle.

Let $\pi =3.14$

$A_{square}= s^{2} = (6)^{2} = 36 in^{2}$

$A_{circle}= \pi r^{2}=3.14\cdot3^{2}=3.14\cdot9=28.26 in^{2}$

So the approximate difference is in area $8\ \textup{in}^{2}$

Report an Error

Example Question #231 : High School Math

Two equal circles are cut out of a rectangular sheet of paper with the dimensions 10 by 20. The circles were made to have the greatest possible diameter. What is the approximate area of the paper after the two circles have been cut out?

Figure_2

Possible Answers:

Correct answer:

Explanation:

The length of 20 represents the diameters of both circles. Each circle has a diameter of 10 and since radius is half of the diameter, each circle has a radius of 5. The area of a circle is A = πr² . The area of one circle is 25π. The area of both circles is 50π. The area of the rectangle is (10)(20) = 200. 200 - 50π gives you the area of the paper after the two circles have been cut out. π is about 3.14, so 200 – 50(3.14) = 43.

Report an Error

Example Question #232 : High School Math

Screen_shot_2013-03-18_at_10.29.01_pm

Kate has a ring-shaped lawn which has an inner radius of 10 feet and an outer radius 25 feet. What is the area of her lawn?

Possible Answers:

525π ft²

275π ft²

125π ft²

175π ft²

325π ft²

Correct answer:

525π ft²

Explanation:

The area of an annulus is

$\pi (R^{2}-r^{2})$

where is the radius of the larger circle, and is the radius of the smaller circle.

$\pi (25^{2}-10^{2})$

$\pi (625-100)$

$525\pi$

Report an Error

Example Question #233 : High School Math

A 6 by 8 rectangle is inscribed in a circle. What is the area of the circle?

Possible Answers:

$25\pi$

$10\pi$

$4\pi$

$20\pi$

Correct answer:

$25\pi$

Explanation:

The image below shows the rectangle inscribed in the circle. Dividing the rectangle into two triangles allows us to find the diameter of the circle, which is equal to the length of the line we drew. Using a²+b²= c² we get 6²+ 8² = c². c² = 100, so c = 10. The area of a circle is $A=\pi r^2$ . Radius is half of the diameter of the circle (which we know is 10), so r = 5.

$A=\pi *5^2=25\pi$

Diagram_1

Report an Error

View SAT Mathematics Tutors

Joy
Certified Tutor

Boston University, Bachelor in Arts, Conservation Biology.

View SAT Mathematics Tutors

Sharif
Certified Tutor

NCCU, Bachelors, Physics and Mathematics.

View SAT Mathematics Tutors

Miriam
Certified Tutor

Washington University in St Louis, Bachelor in Arts, Biology, General.

All SAT Math Resources

16 Diagnostic Tests 660 Practice Tests Question of the Day Flashcards Learn by Concept

SAT Math Tutors in Top Cities:

Atlanta SAT Math Tutors, Austin SAT Math Tutors, Boston SAT Math Tutors, Chicago SAT Math Tutors, Dallas Fort Worth SAT Math Tutors, Denver SAT Math Tutors, Houston SAT Math Tutors, Kansas City SAT Math Tutors, Los Angeles SAT Math Tutors, Miami SAT Math Tutors, New York City SAT Math Tutors, Philadelphia SAT Math Tutors, Phoenix SAT Math Tutors, San Diego SAT Math Tutors, San Francisco-Bay Area SAT Math Tutors, Seattle SAT Math Tutors, St. Louis SAT Math Tutors, Tucson SAT Math Tutors, Washington DC SAT Math Tutors

Popular Courses & Classes

GRE Courses & Classes in Boston, SSAT Courses & Classes in New York City, MCAT Courses & Classes in Los Angeles, GMAT Courses & Classes in Dallas Fort Worth, LSAT Courses & Classes in San Diego, GRE Courses & Classes in Phoenix, GRE Courses & Classes in San Francisco-Bay Area, GMAT Courses & Classes in Chicago, SSAT Courses & Classes in San Francisco-Bay Area, MCAT Courses & Classes in Washington DC

Popular Test Prep

SAT Test Prep in Seattle, ISEE Test Prep in San Diego, GRE Test Prep in San Francisco-Bay Area, ISEE Test Prep in Miami, ACT Test Prep in Philadelphia, LSAT Test Prep in Phoenix, GRE Test Prep in Washington DC, LSAT Test Prep in San Diego, GRE Test Prep in Houston, GMAT Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT Math : Circles

Study concepts, example questions & explanations for SAT Math

All SAT Math Resources

Example Questions

Example Question #28 : How To Find The Area Of A Circle

Example Question #31 : Radius

Example Question #32 : Radius

Example Question #33 : Radius

Example Question #34 : Radius

Example Question #41 : Radius

Example Question #42 : Radius

Example Question #231 : High School Math

Example Question #232 : High School Math

Example Question #233 : High School Math

All SAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: