All SAT Math Resources
Example Questions
Example Question #1 : How To Find The Angle Of A Sector
What is the angle of a sector that has an arc length of 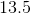



The first thing to do for this problem is to compute the total circumference of the circle. Notice that you were given the diameter. The proper equation is therefore:
For your data, this means,
Now, to compute the angle, note that you have a percentage of the total circumference, based upon your arc length:
Rounded to the nearest hundredth, this is 
Example Question #2 : How To Find The Angle Of A Sector

Figure NOT drawn to scale.
Refer to the above diagram.

Insufficient information is given to answer the question.
An inscribed angle of a circle that intercepts a semicircle is a right angle; therefore, 




The measure of inscribed 

An inscribed angle of a circle intercepts an arc of twice its degree measure, so

Example Question #3 : How To Find The Angle Of A Sector
 Figure NOT drawn to scale
Figure NOT drawn to scale
Refer to the above figure. 




or, equivalently,
In terms of 



Setting 


Example Question #4 : How To Find The Angle Of A Sector

Refer to the above diagram. Evaluate the measure of 
The total measure of the arcs that comprise a circle is 
Substituting the appropriate expression for each arc measure:
Therefore,

and
The measure of the angle formed by the tangent segments 


Substituting:
Example Question #31 : Circles

Figure NOT drawn to scale.
The above figure shows a quadrilateral inscribed in a circle. Evaluate 
The question cannot be answered from the information given.
If a quadrilateral is inscribed in a circle, then each pair of its opposite angles are supplementary - that is, their degree measures total 


Setting 



the correct response.
Example Question #31 : Circles

Figure NOT drawn to scale.
The above figure shows a quadrilateral inscribed in a circle. Evaluate 
The question cannot be answered from the information given.
The question cannot be answered from the information given.
If a quadrilateral is inscribed in a circle, then each pair of its opposite angles are supplementary - that is, their degree measures total 


Setting 



The statement turns out to be true regardless of the value of 

Example Question #281 : Sat Mathematics

Figure NOT drawn to scale.
The above figure shows a quadrilateral inscribed in a circle. Evaluate 
If a quadrilateral is inscribed in a circle, then each pair of its opposite angles are supplementary - that is, their degree measures total 


Setting 



the correct response.
Example Question #282 : Geometry

Figure NOT drawn to scale.
Refer to the above diagram. 



If we let 

and
If a secant and a tangent are drawn from a point to a circle, the measure of the angle they form is half the difference of the measures of the intercepted arcs. Since 



Setting 


The inscribed angle that intercepts this arc, 

This is the correct response.
Example Question #284 : Geometry
 Figure NOT drawn to scale.
Figure NOT drawn to scale.
In the above figure, 



The measure of 



If we let 

and
the ratio of the length of 

Setting 

Cross-multiply, then solve for 

If a secant and a tangent are drawn from a point to a circle, the measure of the angle they form is half the difference of the measures of the intercepted arcs. Since 




Example Question #31 : Circles
If the area of a circle is four times larger than the circumference of that same circle, what is the diameter of the circle?
16
32
2
4
8
16
Set the area of the circle equal to four times the circumference πr2 = 4(2πr).
Cross out both π symbols and one r on each side leaves you with r = 4(2) so r = 8 and therefore d = 16.
All SAT Math Resources


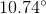




























![\frac{1}{2}\left [ (180 - t) - t \right ]= 34](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/790827/gif.latex)























































![\frac{1}{2} [ \left ( 180-t \right ) - t ] = 28](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/814539/gif.latex)



























