SAT Math : Circles
Study concepts, example questions & explanations for SAT Math
All SAT Math Resources
Example Questions
Example Question #11 : How To Find The Length Of The Diameter
Give the diameter of a circle with radius forty-two inches.
None of these
The diameter of a circle is twice its radius, so if a circle has radius 42 inches, its diameter is
Divide by 12 to convert to feet:
Example Question #1 : How To Find The Ratio Of Diameter And Circumference
Let 
The formula for the area of a circle is 
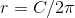
We can then substitute this value of r into the formula for the area:
Example Question #2 : How To Find The Area Of A Circle
If a circle has circumference 
If the circumference is 
Example Question #1 : Radius
If the equation of a circle is (x – 7)2 + (y + 1)2 = 81, what is the area of the circle?
49π
6561π
18π
2π
81π
81π
The equation is already in a circle equation, and the right side of the equation stands for r2 → r2 = 81 and r = 9
The area of a circle is πr2, so the area of this circle is 81π.
Example Question #1 : Radius
Assume π = 3.14
A man would like to put a circular whirlpool in his backyard. He would like the whirlpool to be six feet wide. His backyard is 8 feet long by 7 feet wide. By state regulation, in order to put a whirlpool in a backyard space, the space must be 1.5 times bigger than the pool. Can the man legally install the whirlpool?
No, because the area of the whirlpool is 42.39 square feet and 1.5 times its area would be greater than the area of the backyard.
No, because the area of the backyard is smaller than the area of the whirlpool.
Yes, because the area of the whirlpool is 18.84 square feet and 1.5 times its area would be less than the area of the backyard.
No, because the area of the backyard is 30 square feet and therefore the whirlpool is too big to meet the legal requirement.
Yes, because the area of the whirlpool is 28.26 square feet and 1.5 times its area would be less than the area of the backyard.
Yes, because the area of the whirlpool is 28.26 square feet and 1.5 times its area would be less than the area of the backyard.
If you answered that the whirlpool’s area is 18.84 feet and therefore fits, you are incorrect because 18.84 is the circumference of the whirlpool, not the area.
If you answered that the area of the whirlpool is 56.52 feet, you multiplied the area of the whirlpool by 1.5 and assumed that that was the correct area, not the legal limit.
If you answered that the area of the backyard was smaller than the area of the whirlpool, you did not calculate area correctly.
And if you thought the area of the backyard was 30 feet, you found the perimeter of the backyard, not the area.
The correct answer is that the area of the whirlpool is 28.26 feet and, when multiplied by 1.5 = 42.39, which is smaller than the area of the backyard, which is 56 square feet.
Example Question #2 : How To Find The Area Of A Circle
There are two identical circles on a plane that overlap. The radius of both circles is 1. The region in which they overlap has an area of π.
What is the total area of the 2 overlapping circles?
2π
1
π
2
0
π
The total area of both circles is π + π = 2π
Since the region overlaps, we cannot count it twice, so we must subtract it.
we get 2π – π = π
Example Question #3 : How To Find The Area Of A Circle
A square with a side length of 4 inches is inscribed in a circle, as shown below. What is the area of the unshaded region inside of the circle, in square inches?
8π - 16
8π-8
2π-4
4π-4
8π-4
8π - 16
Using the Pythagorean Theorem, the diameter of the circle (also the diagonal of the square) can be found to be 4√2. Thus, the radius of the circle is half of the diameter, or 2√2. The area of the circle is then π(2√2)2, which equals 8π. Next, the area of the square must be subtracted from the entire circle, yielding an area of 8π-16 square inches.
Example Question #1 : Radius
If a circle has a circumference of 16π, what would its area be if its radius were halved?
16π
64π
4π
8π
16π
The circumference of a circle = πd where d = diameter. Therefore, this circle’s diameter must equal 16. Knowing that diameter = 2 times the radius, we can determine that the radius of this circle = 8. Halving the radius would give us a new radius of 4. To find the area of this new circle, use the formula A=πr² where r = radius. Plug in 4 for r. Area will equal 16π.
Example Question #51 : Circles
A star is inscribed in a circle with a diameter of 30, given the area of the star is 345, find the area of the shaded region, rounded to one decimal.
341.5
361.5
346.5
356.5
351.5
361.5
The area of the circle is (30/2)2*3.14 (π) = 706.5, since the shaded region is simply the area difference between the circle and the star, it’s 706.5-345 = 361.5
Example Question #72 : Circles
The diameter of a circle increases by 100 percent. If the original area is 16π, what is the new area of the circle?
49π
54π
50π
64π
160π
64π
The original radius would be 4, making the new radius 8 and by the area of a circle (A=π(r)2) the new area would be 64π.
All SAT Math Resources
