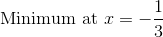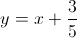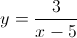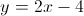Rewrite the equation by the order of powers.

This is a parabola in standard form:  

Determine the values of 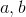 to the vertex formula.

Since the leading coefficient of the parabola is negative, the parabola will curve downward and will have a maximum point.  

Therefore there is a maximum at,

 .

First, subtract 7 to both sides.

Factor the y on the left hand side.

Divide both sides by 3 – x.

Take an extra step by factoring the minus sign on the denominator.

Cancel the minus signs.

Let .

First, calculate the slope between the two points.

Next, use the slope-intercept form to calculate the intercept. We are able to plug in our value for the slope, as well the the values for .

Using slope-intercept form, where we know and , we can see that the equation for this line is .

To calculate a line passing through two points, we first need to calculate the slope, .

Now that we have the slope, we can plug it into our equation for a line in slope intercept form.

To solve for , we can plug in one of the points we were given. For the sake of this example, let's use , but realize either point will give use the same answer.

Now that we have solved for b, we can plug that into our slope intercept form and produce and the answer

We are looking for a point, , where these two lines intersect. While there are many ways to solve for and given two equations, the simplest way I see is to use the elimination method since by adding the two equations together, we can eliminate the variable.

Dividing both sides by 7, we isolate y.

Now, we can plug y back into either equation and solve for x.

Next, we can solve for x.

Therefore, the point where these two lines intersect is .

The first thing is to plug in the given value so you equation is 

.  

Then you must subtract  from both sides in order to get  by itself.  

You now have 

and you must multiply by  for each side and you get .

Add  on both sides.

Subtract 2 from both sides.

Divide by 10 on both sides.

Reduce the fractions.

The answer is:  

Distribute the right side.

Rewrite the equation.

Subtract  on both sides.

Add 4 on both sides.

Divide by three on both sides.

The answer is:  

You must get  by itself so you must add  to both side which results in 

.  

You must get the square root of both side to undue the exponent.  

This leaves you with .  

But since you square the  in the equation, the original value you plug can also be its negative value since squaring it will make it positive anyway.  

This means your answer can be  or .

The asymptote of this equation can be found by observing that  regardless of . We are thus solving for the value of as approaches zero.

So the value that  cannot exceed is , and the line  is the asymptote.