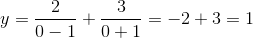Call Now to Set Up Tutoring:

(888) 888-0446

SAT II Math I : Functions and Graphs

Study concepts, example questions & explanations for SAT II Math I

Create An Account

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #6 : X Intercept And Y Intercept

Find the -intercepts of the following equation:

y^2+x+5y=3x^2-2

Round each of your answers to the nearest tenth.

Possible Answers:

-5.2 and -3.1

1.5 and 2.4

-4.4 and 1.7

5.2 and 8.9

-4.6 and -0.4

Correct answer:

-4.6 and -0.4

Explanation:

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting for . Then, we need to get it into standard form:

y^2+0+5y=3(0)^2-2

y^2+5y=-2

y^2+5y+2=0

Recall that the general form of the quadratic formula is:

$\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

Based on our equations, the following are your formula values:

a = 1

b = 5

c=2

Therefore, the quadratic formula will be:

$\frac{-5\pm\sqrt{5^2-4(1)(2)}}{2(2)}$

Simplifying, you get:

$\frac{-5\pm\sqrt{25-8}}{4}$

$\frac{-5\pm\sqrt{17}}{4}$

Using a calculator, you will get:

-4.561552812808831 and -0.43844718719117

Report an Error

Example Question #4 : X Intercept And Y Intercept

What is the -intercept of the following equation?

44x-2y=120+4x

Possible Answers:

None of the others

Correct answer:

Explanation:

The easiest way to solve for this kind of simple -intercept is to set equal to . You can then solve for the value in order to find the relevant intercept.

44x-2(0)=120+4x

44x=120+4x

Solve for :

40x = 120

Divide both sides by 40:

x = 3

Report an Error

Example Question #1 : X Intercept And Y Intercept

y=15x-30

What is the x-intercept of the above equation?

Possible Answers:

Correct answer:

Explanation:

To find the x-intercept, you must plug in for .

This gives you,

0=15x-30 and you must solve for .

First, add to both sides which gives you,

30=15x .

Then divide both sides by to get,

x=2 .

Report an Error

Example Question #8 : X Intercept And Y Intercept

Find the -intercepts of the following equation:

x^2+(y+14)^2 = 25

Round each of your answers to the nearest tenth.

Possible Answers:

11.0 and 36.0

-16.4 and 12.5

5.5 and 12.4

-5.0 and 5.0

-19.0 and -9.0

Correct answer:

-19.0 and -9.0

Explanation:

There are two ways to solve this. First, you could substitute in for :

0^2+(y+14)^2 = 25

Take the square-root of both sides and get:

$y+14 = \pm5$

$y= -14\pm5$

Therefore, your two answers are and .

You also could have done this by noticing that the problem is a circle of radius , shifted downward by .

Report an Error

Example Question #8 : X Intercept And Y Intercept

What is the x-intercept of the given equation? 2x+3y = 1

Possible Answers:

$-\frac{1}{3}$

$-\frac{1}{2}$

$\frac{1}{6}$

$\frac{1}{2}$

Correct answer:

$\frac{1}{2}$

Explanation:

In order to determine the x-intercept, we will need to let y=0 , and solve for .

2x+3(0) = 1

2x=1

Divide both sides by two.

$\frac{2x}{2}=\frac{1}{2}$

The answer is: $\frac{1}{2}$

Report an Error

Example Question #31 : Properties Of Functions And Graphs

What is the y-intercept of the function? $y=\frac{2}{x-1}+\frac{3}{x+1}$

Possible Answers:

$\frac{1}{5}$

$\textup{Does not exist.}$

Correct answer:

Explanation:

The y-intercept is the value of when x=0 .

Substitute zero into the x-variable in the equation.

$y=\frac{2}{0-1}+\frac{3}{0+1} = -2+3 = 1$

The y-intercept is .

The answer is:

Report an Error

Example Question #1 : Slope

What is the slope of the line depicted by this equation?

$\small 4x+5y=14$

Possible Answers:

$\small \frac{14}{5}$

$\small \frac{5}{4}$

$\small \frac{4}{5}$

$\small -\frac{4}{5}$

Correct answer:

$\small -\frac{4}{5}$

Explanation:

This equation is written in standard form, that is, $\small Ax+By=C$ where the slope is equal to $\small \frac{-A}{B}$ .

$\small 4x+5y=14$

In this instance $\small A=4$ and $\small B=5$

$m=-\frac{A}{B}=-\frac{4}{5}$

This question can also be solved by converting the slope-intercept form: $\small y=-\frac{4}{5}x+\frac{14}{5}$ .

Report an Error

Example Question #2 : Slope

Find the slope of the line

4x+3y=-12

Possible Answers:

$\frac{-3}{4}$

$\frac{4}{3}$

$\frac{3}{4}$

$\frac{-4}{3}$

Correct answer:

$\frac{-4}{3}$

Explanation:

To find the slope of any line, we must get the equation into the form

y=mx+b

where m is the slope and b is the y-intercept.

To manipulate our equation into this form, we must solve for y. First, we must move the x term to the right side of our equation by subtracting it from both sides.

(4x+3y)-4x = (-12)-4x

3y = -4x-12

To isolate y, we now must divide each side by 3.

$\frac{3y}{3}=\frac{-4x}{3}-\frac{12}{3}$

$y=\frac{-4}{3}x-4$

Now our equation is in the desired form. The coefficient of our x term is our slope, . Therefore

$m = \frac{-4}{3}$

Report an Error

Example Question #1 : Slope

$\frac{y}{2}=5x-1$

What is the slope of the function above?

Possible Answers:

Correct answer:

Explanation:

First you must get the formula into slope-intercept form which means having by itself,

y=mx+b where is the slope.

You must multiple both sides by to get,

y=10x-2 .

The slope is the value being multiplied by the variable, so our slope is .

Report an Error

Example Question #4 : Slope

Find the slope of the following equation: 3x+3y =1

Possible Answers:

$-\frac{1}{3}$

$\frac{1}{3}$

Correct answer:

Explanation:

In order to find the slope, we will need to rearrange the equation so that it is in slope-intercept form y=mx+b .

Subtract on both sides.

3x+3y -3x=1-3x

3y=-3x+1

Divide by three on both sides.

$\frac{3y}{3}=\frac{-3x+1}{3}$

$y=-x + \frac{1}{3}$

This equation is now in the form of y=mx+b , where is the slope.

The slope is .

Report an Error

View SAT Subject Test in Mathematics Level 1 Tutors

Sumit
Certified Tutor

Calcutta University, Bachelor of Science, Mathematics. Indian Statistical Institute, Master of Science, Mathematics.

View SAT Subject Test in Mathematics Level 1 Tutors

Braeden
Certified Tutor

Vanderbilt University, Bachelor in Arts, Mathematics and Computer Science.

View SAT Subject Test in Mathematics Level 1 Tutors

Liban
Certified Tutor

Emory University, Bachelor of Science, Mathematics/Economics.

All SAT II Math I Resources

6 Diagnostic Tests 113 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

GMAT Tutors in Boston, Biology Tutors in Atlanta, Biology Tutors in Houston, ACT Tutors in Chicago, ACT Tutors in Los Angeles, English Tutors in Boston, ACT Tutors in Boston, SAT Tutors in Dallas Fort Worth, Algebra Tutors in Miami, Computer Science Tutors in Philadelphia

Popular Courses & Classes

Spanish Courses & Classes in Phoenix, GRE Courses & Classes in Denver, LSAT Courses & Classes in Chicago, ISEE Courses & Classes in Miami, SAT Courses & Classes in Boston, ACT Courses & Classes in Los Angeles, MCAT Courses & Classes in Denver, Spanish Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in New York City, GMAT Courses & Classes in Washington DC

Popular Test Prep

ISEE Test Prep in Miami, LSAT Test Prep in Philadelphia, ACT Test Prep in Los Angeles, GMAT Test Prep in Washington DC, ACT Test Prep in Boston, SAT Test Prep in Miami, LSAT Test Prep in Houston, SSAT Test Prep in Phoenix, SSAT Test Prep in Philadelphia, MCAT Test Prep in Boston

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

SAT II Math I : Functions and Graphs

Study concepts, example questions & explanations for SAT II Math I

All SAT II Math I Resources

Example Questions

Example Question #6 : X Intercept And Y Intercept

Example Question #4 : X Intercept And Y Intercept

Example Question #1 : X Intercept And Y Intercept

Example Question #8 : X Intercept And Y Intercept

Example Question #8 : X Intercept And Y Intercept

Example Question #31 : Properties Of Functions And Graphs

Example Question #1 : Slope

Example Question #2 : Slope

Example Question #1 : Slope

Example Question #4 : Slope

All SAT II Math I Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: