Finding the Domain

The domain of a function is defined as the set of all valid input values of  overwhich the function is defined. The simple rule of thumb for rational functions is that all real numbers will work except for those in which denominator is zero since division by zero is not allowed.

Set the denominator to zero and solve for , 

The function is therefore defined everywhere except at . Therefore the domain expressed in interval notation is,

Note that the open parentheses indicate that  is not in the domain, but  may become arbitrarily close to  . 

Finding the Range 

The range of a function is defined as the set of all outputs spanning the domain. Finding the range can be achieved by finding the domain of the inverse function. First solve   for  to obtain the inverse function, 

Multiply both sides by , 

Distribute , 

Move all terms with  to one side of the equation, 

Factor and solve for 

The inverse function is therefore,

Find the domain of the inverse function, 

The range of  is the domain of , which is:

If you look at the plots for the function  (in blue) and  (in red and labeled as  in the figure) you can see the asymptotic behavior of as  approaches  and of  as  approaches .

To determine the domain of the function, we must ask ourselves where x can and cannot exist. On the numerator, nothing is preventing x from existing anywhere. But the denominator of the function cannot equal zero (which would produce an undefined value for the function), so to determine at which x values this occurs, we must set the denominator equal to zero and solve for x:

(The factors of 6 that add up to 5 are 3 and 2.)

Because these are the only values that x equal for the function to exist, we make our intervals as shown below:

We use round brackets to indicate that we never include the bounds of the intervals in the domain.

To determine the domain of the function, we must consider where x cannot exist. The only limitation on the function is the denominator, which cannot equal zero. 

To find the x-values where this occurs, we must set the denominator equal to zero and solve for x:

These are the only two limitations on the domain of the function, so the domain of the function is

Note that round brackets were used for all of the intervals, because none of the bounds of the intervals are included in the domain.

To determine the domain of the function, we must find the x-values that would give us an undefined result when we plug them into the function. On the numerator, we know that the natural log function can never equal zero or be negative. In the denominator, we can never have a zero. With these conditions in mind, we must now find the x values that makes these undefined situations occur.

For the numerator:

 and 

For the denominator:

Now that we know where x cannot be, we can now write the domain, making sure to use round brackets for the endpoints of the intervals:

The domain refers to all the possible x-values that can be existent on the given function.  Do not confuse this with the range, since this represents all the existent y-values on the graph.

Since there are no discontinuities for any x-value that we may substitute, the domain is all real numbers.

The answer is:  

To find the y-intercept of any line, we must get the equation into the form

where m is the slope and b is the y-intercept.

To manipulate our equation into this form, we must solve for y. First, we must move the x term to the right side of our equation by subtracting it from both sides.

To isolate y, we now must divide each side by 3.

Now that our equation is in the desired form, our y-intercept is simply

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting  for :

Recall that the general form of the quadratic formula is:

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

Simplifying, you get:

Using a calculator, you will get:

 and 

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting  for :

Recall that the general form of the quadratic formula is:

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

Simplifying, you get:

Using a calculator, you will get:

 and 

For an equation like this, you should use the quadratic formula to solve for the roots. We can easily get our equation into proper form by substituting  for . Then, we need to get it into standard form:

Recall that the general form of the quadratic formula is:

Based on our equations, the following are your formula values:

Therefore, the quadratic formula will be:

Simplifying, you get:

Using a calculator, you will get:

 and 

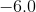
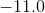
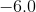
There are two ways to solve this. First, you could substitute in  for :

Take the square-root of both sides and get:

Therefore, your two answers are  and .

You also could have done this by noticing that the problem is a circle of radius , shifted upward by .