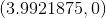All SAT II Math I Resources
Example Questions
Example Question #351 : Sat Subject Test In Math I
Give the 

The graph has no 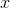
The graph has no 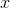
Set 
We need not work further. It is impossible to raise a positive number 2 to any real power to obtain a negative number. Therefore, the equation has no solution, and the graph of 

Example Question #21 : Solving Exponential Functions
What is/are the asymptote(s) of the graph of the function 

An exponential function of the form
has as its one and only asymptote the horizontal line 
Since we define 

then 
and the only asymptote is the line of the equation 
Example Question #22 : Solving Exponential Functions
Determine whether each function represents exponential decay or growth.
a) decay
b) decay
a) decay
b) growth
a) growth
b) decay
a) growth
b) growth
a) decay
b) growth
a)
This is exponential decay since the base, 


b)
This is exponential growth since the base, 

Example Question #4 : Graphing Exponential Functions
Match each function with its graph.
1.
2.
3.
a.
b.
c.
1.
2.
3.
1.
2.
3.
1.
2.
3.
1.
2.
3.
1.
2.
3.
For 





For 



For 



Example Question #5 : Graphing Exponential Functions
An exponential funtion 







To determine the constant 







To find 








We can write our equation as 


Then 
Our model equation is 
Example Question #71 : Functions And Graphs
In 2010, the population of trout in a lake was 416. It has increased to 521 in 2015.
Write an exponential function of the form 

We need to determine the constants 




To get 



Using a calculator, 

Then our model equation for the fish population is
Example Question #7 : Graphing Exponential Functions
What is the 

The 



Thus, to find the 

In this case, you will get,

Example Question #8 : Graphing Exponential Functions
What is the 

There is no 
The 


Thus, to find the 


Thus, we get:
Example Question #21 : Solving Exponential Functions
What is the 

The 

Substituting this in to our funciton, we get:
Example Question #10 : Graphing Exponential Functions
Which of the following functions represents exponential decay?
Exponential decay describes a function that decreases by a factor every time 

These can be recognizable by those functions with a base which is between 

The general equation for exponential decay is,



Thus, we are looking for a fractional base.
The only function that has a fractional base is,

All SAT II Math I Resources