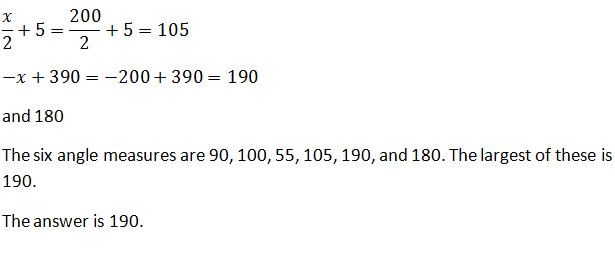Call Now to Set Up Tutoring:

(888) 888-0446

PSAT Math : PSAT Mathematics

Study concepts, example questions & explanations for PSAT Math

Create An Account

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Example Questions

Example Question #581 : Geometry

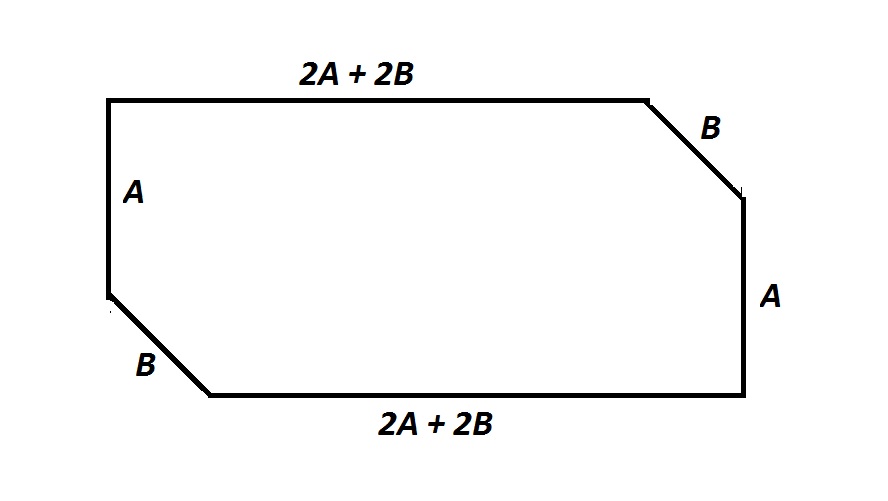
Hexagon

Note: Figure NOT drawn to scale.

The perimeter of the above hexagon is 888. Also, A-B = 10 . Evaluate .

Possible Answers:

A = 79

$A = 93\frac{4}{5}$

$A = 60\frac{1}{2}$

Insufficient information is given to answer the problem.

A = 116

Correct answer:

A = 79

Explanation:

The perimeter of the figure can be expressed in terms of the variables by adding:

$A + B + A + B + \left (2A + 2B \right ) + \left (2A + 2B \right ) = P$

Simplify and set P = 888 :

A + A + 2A + 2A + B+ B +2B + 2B= 888

6A + 6B= 888

$6\left (A + B \right )= 888$

A + B = 148

Along with A-B = 10 , we now have a system of equations to solve for by adding:

A + B = 148

$\underline{A-B =\; 10}$

$2A = \; \; \; \; \; \; 158$

A = 79

Report an Error

Example Question #1 : How To Find The Length Of The Side Of A Hexagon

Hexagon

Note: Figure NOT drawn to scale.

The perimeter of the above figure is 132. What is A + B ?

Possible Answers:

$26\frac{2}{5}$

$16 \frac{1}{2}$

Correct answer:

Explanation:

The perimeter of the figure can be expressed in terms of the variables by adding:

$A + B + A + B + \left (2A + 2B \right ) + \left (2A + 2B \right ) = P$

Simplify and set P = 132 :

A + A + 2A + 2A + B+ B +2B + 2B= 132

6A + 6B= 132

$6\left (A + B \right )= 132$

A + B = 22

Report an Error

Example Question #581 : Geometry

Hexagon

Note: Figure NOT drawn to scale.

The perimeter of the above figure is 600. The ratio of to is 3:2 . Evaluate .

Possible Answers:

B = 40

B = 72

B = 60

B = 48

B = 100

Correct answer:

B = 40

Explanation:

The perimeter of the figure can be expressed in terms of the variables by adding:

$A + B + A + B + \left (2A + 2B \right ) + \left (2A + 2B \right ) = P$

Simplify and set P = 600 :

A + A + 2A + 2A + B+ B +2B + 2B= 600

6A + 6B= 600

Since the ratio of to is equivalent to 3:2 - or

$\frac{A}{B} = \frac{3}{2}$ ,

then

$A = \frac{3}{2} B$

and we can substitute as follows:

$6 \cdot \frac{3}{2}B + 6B= 600$

9B + 6B= 600

15B = 600

B = 40

Report an Error

Example Question #1 : How To Find An Angle In A Hexagon

Possible Answers:

190

180

200

170

210

Correct answer:

190

Explanation:

Report an Error

Example Question #1 : How To Find An Angle In A Hexagon

If a triangle has 180 degrees, what is the sum of the interior angles of a regular octagon?

Possible Answers:

1080

900

720

540

1260

Correct answer:

1080

Explanation:

The sum of the interior angles of a polygon is given by 180(n - 2) where = number of sides of the polygon. An octagon has 8 sides, so the formula becomes 180(8 -2) = 1080

Report an Error

Example Question #1 : How To Find An Angle In A Hexagon

In a rectangular hexagon, what is the meaure of each interior angle?

Possible Answers:

120 degrees

90 degrees

105 degrees

150 degrees

72 degrees

Correct answer:

120 degrees

Explanation:

The sum of the interior angles of a hexagon must equal 720 degrees. Because the hexagon is regular, all of the interior angles will have the same measure. A hexagon has six sides and six interior angles. Therefore, each angle measures $\frac{720}{6}=120$ .

Report an Error

Example Question #1 : How To Find An Angle In A Hexagon

Hexagon

Note:Figure NOT drawn to scale.

Refer to the above figure. Evaluate .

Possible Answers:

x = 130

x = 140

x = 100

x = 110

x = 120

Correct answer:

x = 130

Explanation:

The sum of the degree measures of the angles of a (six-sided) hexagon, is

$180 ^{\circ } \times (6 - 2) = 180 ^{\circ } \times 4 = 720^{\circ }$

We can solve for in the equation

x + 92 + 164 + 90 + 137 + 107 = 720

x +590 = 720

x = 130

Report an Error

Example Question #581 : Geometry

Hexagon

Note: Figure NOT drawn to scale.

Refer to the above figure. Evaluate .

Possible Answers:

x = 101

x = 111

x = 106

x = 116

x = 121

Correct answer:

x = 111

Explanation:

The sum of the degree measures of the angles of a (six-sided) hexagon, is

$180 ^{\circ } \times (6 - 2) = 180 ^{\circ } \times 4 = 720^{\circ }$

We can solve for in the equation

x + x+ 164 + 90 + 137 + 107 = 720

2x + 498 = 720

2x = 222

x=111

Report an Error

Example Question #582 : Geometry

Three angles of a hexagon measure $65^{\circ}, 74^{\circ}, 89^{\circ}$ . The other three angles are congruent to one another. What is the measure of each of the latter three angles?

Possible Answers:

This hexagon cannot exist.

$164^{\circ}$

$174^{\circ}$

$48^{\circ}$

$58^{\circ}$

Correct answer:

$164^{\circ}$

Explanation:

The sum of the degree measures of the angles of a (six-sided) hexagon, is

$180 ^{\circ } \times (6 - 2) = 180 ^{\circ } \times 4 = 720^{\circ }$

Let be the common measure of the three congruent angles in question. We can solve for in the equation

x + x + x + 65+ 74 + 89 = 720

3 x + 228 = 720

3 x = 492

x = 164

Report an Error

Example Question #1 : How To Find An Angle In A Hexagon

What is the measurement of one of the interior angles of a regular hexagon?

Possible Answers:

$150^\circ$

$120^\circ$

$105^\circ$

$135^\circ$

$90^\circ$

Correct answer:

$120^\circ$

Explanation:

To find the sum of the interior angles of any regular polygon, use the formula $(n-2)\cdot180$ , where represents the number of sides of the regular polygon.

$=(6-2)\cdot180$

$=4\cdot180$

=720

The sum of the interior angles of a regular hexagon is 720 degrees. To find the measurement of one angle, divide by the number of interior angles (or sides):

=720/6

=120

The measurement of one angle in a regular hexagon is 120 degrees.

Report an Error

View PSAT Mathematics Tutors

Elvis
Certified Tutor

Methodist University, Bachelor of Science, Mathematics and Computer Science.

View PSAT Mathematics Tutors

Chase
Certified Tutor

Western Governors University, Bachelor of Science, Mathematics.

View PSAT Mathematics Tutors

Leonard
Certified Tutor

Florida State University, Bachelor of Science, Environmental Science.

All PSAT Math Resources

10 Diagnostic Tests 421 Practice Tests Question of the Day Flashcards Learn by Concept

Popular Subjects

Chemistry Tutors in Miami, Calculus Tutors in New York City, ISEE Tutors in Washington DC, English Tutors in Los Angeles, ISEE Tutors in Los Angeles, Reading Tutors in Denver, MCAT Tutors in Chicago, French Tutors in Denver, GMAT Tutors in Seattle, GRE Tutors in Houston

Popular Courses & Classes

Spanish Courses & Classes in Dallas Fort Worth, ACT Courses & Classes in Boston, GMAT Courses & Classes in Miami, ISEE Courses & Classes in Philadelphia, GRE Courses & Classes in Chicago, ACT Courses & Classes in Los Angeles, LSAT Courses & Classes in Philadelphia, SSAT Courses & Classes in Boston, SSAT Courses & Classes in Denver, GRE Courses & Classes in Seattle

Popular Test Prep

SAT Test Prep in Atlanta, ACT Test Prep in Boston, GMAT Test Prep in Miami, LSAT Test Prep in Chicago, GMAT Test Prep in San Diego, GMAT Test Prep in Seattle, ACT Test Prep in Los Angeles, GRE Test Prep in Houston, MCAT Test Prep in San Diego, GRE Test Prep in Miami

DMCA Complaint

If you believe that content available by means of the Website (as defined in our Terms of Service) infringes one or more of your copyrights, please notify us by providing a written notice (“Infringement Notice”) containing the information described below to the designated agent listed below. If Varsity Tutors takes action in response to an Infringement Notice, it will make a good faith attempt to contact the party that made such content available by means of the most recent email address, if any, provided by such party to Varsity Tutors.

Your Infringement Notice may be forwarded to the party that made the content available or to third parties such as ChillingEffects.org.

Please be advised that you will be liable for damages (including costs and attorneys’ fees) if you materially misrepresent that a product or activity is infringing your copyrights. Thus, if you are not sure content located on or linked-to by the Website infringes your copyright, you should consider first contacting an attorney.

Please follow these steps to file a notice:

You must include the following:

A physical or electronic signature of the copyright owner or a person authorized to act on their behalf; An identification of the copyright claimed to have been infringed; A description of the nature and exact location of the content that you claim to infringe your copyright, in \ sufficient detail to permit Varsity Tutors to find and positively identify that content; for example we require a link to the specific question (not just the name of the question) that contains the content and a description of which specific portion of the question – an image, a link, the text, etc – your complaint refers to; Your name, address, telephone number and email address; and A statement by you: (a) that you believe in good faith that the use of the content that you claim to infringe your copyright is not authorized by law, or by the copyright owner or such owner’s agent; (b) that all of the information contained in your Infringement Notice is accurate, and (c) under penalty of perjury, that you are either the copyright owner or a person authorized to act on their behalf.

Send your complaint to our designated agent at:

Charles Cohn Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Or fill out the form below:

Do not fill in this field

Contact Information

* Full legal name

Company name

* Phone number

* Email address

Address

* Address1

Address2

* City

* State

* Zipcode

* Country

Complaint Details

* URL of copyrighted work (where your original material is located)

* Please describe the copyrighted work so that it may be easily identified

I am the owner, or an agent authorized to act on behalf of the owner of an exclusive right that is allegedly infringed.

I have a good faith belief that the use of the material in the manner complained of is not authorized by the copyright owner, its agent, or the law.

This notification is accurate.

I acknowledge that there may be adverse legal consequences for making false or bad faith allegations of copyright infringement by using this process.

* Signature (your digital signature is legally binding)

HIGH SCHOOL

GRADUATE SCHOOL

K-8

Search 50+ Tests

math tutoring

science tutoring

foreign languages

elementary tutoring

other

Search 350+ Subjects

PSAT Math : PSAT Mathematics

Study concepts, example questions & explanations for PSAT Math

All PSAT Math Resources

Example Questions

Example Question #581 : Geometry

Example Question #1 : How To Find The Length Of The Side Of A Hexagon

Example Question #581 : Geometry

Example Question #1 : How To Find An Angle In A Hexagon

Example Question #1 : How To Find An Angle In A Hexagon

Example Question #1 : How To Find An Angle In A Hexagon

Example Question #1 : How To Find An Angle In A Hexagon

Example Question #581 : Geometry

Example Question #582 : Geometry

Example Question #1 : How To Find An Angle In A Hexagon

All PSAT Math Resources

Report an issue with this question

DMCA Complaint

Contact Information

Address

Complaint Details

Email address:
Your name:
Feedback: